#비트연산
우선 비트연산에 대해서 알아보자
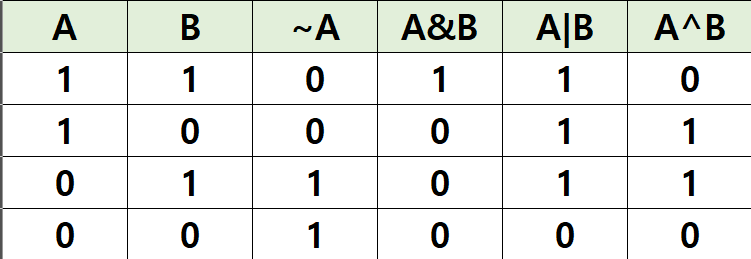
1. NOT 연산 (~)
- ~ (부정): NOT 연산은 단항 연산으로, 각 비트를 반전시킵니다. 즉, 1을 0으로, 0을 1로 바꿉니다.
- 예시:
- 입력: A = 1010 (2진수)
- 결과: ~A = 0101
2. AND 연산 (&)
- & (AND): AND 연산은 두 비트가 모두 1일 때만 1을 반환하고, 나머지 경우에는 0을 반환합니다.
- 진리표:
A B A & B
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- 예시:
- 입력: A = 1100, B = 1010
- 결과: A & B = 1000
3. OR 연산 (|)
- | (OR): OR 연산은 두 비트 중 하나라도 1이면 1을 반환하고, 둘 다 0일 때만 0을 반환합니다.
- 진리표:
ABA | B
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- 예시:
- 입력: A = 1100, B = 1010
- 결과: A | B = 1110
4. XOR 연산 (^)
- ^ (XOR): XOR 연산은 두 비트가 서로 다를 때만 1을 반환하고, 같을 때는 0을 반환합니다.
- 진리표:
A B A ^ B
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
- 예시:
- 입력: A = 1100, B = 1010
- 결과: A ^ B = 0110
#Left Shift
비트를 좌측으로 옮길 경우에는
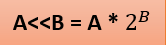
2제곱을 곱해주는 효과가 있다.
예를 들어서
1 << 2

인 경우에는 연산 결과로

1 * 2^2
로 4가 되는걸 확인 할 수 있다.
좀 더 확인해보자면
3 << 3
결과값으론

2*3^3 = 24 가 된다는걸 알 수 있다.
#Right Shift
비트를 우측으로 옮길 경우에는
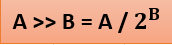
반대로 2 제곱을 나눠주는 효과가 있다
10>>2 인경우
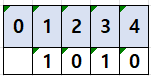
결과값으로 10/2^2 한 값인 2가 나오는걸 알 수있다.

#Shift 활용
shift 연산을 활용하면

중간값을 구하는 과정을 매우 빠르게 할 수 있다. ( >> 1) 을 활용해서
그리고 홀수 인지 판별하는 경우도 1과의 and 연산을 빠르게 해줄 수 있다.
왜냐면 홀수인 경우에는 가장 작은 비트가 1이기 때문에 & 1 연산을 해주면
1이 나오고 짝수인 경우에는 &1 연산이후에 0이기 때문에
- 짝수: 마지막 비트(Least Significant Bit, LSB) 0이다.
- 예: 2 (10₂), 4 (100₂), 6 (110₂)
- 홀수: 마지막 비트(LSB)가 1이다.
- 예: 1 (1₂), 3 (11₂), 5 (101₂)
빠르게 구할 수 있다.
#비트마스크 Bit Mask
비트 마스크에 대해서 알아보자
비트 마스크는
특정 상태나 값이 들어있는지 확인하는데 유용하다
특히 방문배열 을 활용한 dfs 나 bfs 구현에서 유용하게 사용 할 수 있다.
예를 들어서
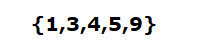
의 배열을 가지고 있다면
1번 3번 4번 5번 9번을 방문했기때문에
이진수로 바꿔서 더해주게 되면
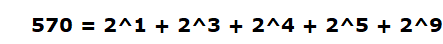
가 되고
이 배열들의 인덱스에 값들이 들어가 있는걸 확인 할 수 있다
&연산을 통해서
그 위치의 이진수가 존재하는지 확인해 주면 된다
특정 자리에 값이 있는지 확인하고 싶은 경우 (특정 순서의 비트에 값이 있는지 확인)
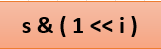
원하는 위치만큼 1을 << 연산 해주고
&연산을 해주게 되면 1을 반환하면 그 자리에 존재하고
0을 반환하면 그 값이 없다는걸 알 수 잇다.

2가 들어있는지 알고싶기 때문에 1을 <<1 연산을 하고 & 연산을 하면

가 나오기 때문에 2가 비트마스크에 들어있다는 것을 알 수 있다.
즉 값의 인덱스에 존재하는지 알고싶다면 2진수로 변환한 뒤에
&연산을해서 그값이 똑같이 나온다면 존재한다는 것이다.
#비트마스크 Bit Mask 추가
비트 마스크는
| or 연산을 해서 추가해 줄 수 있다.
특정 인덱스 추가해주는경우

원하는 위치만큼 1 을 << 연산을 해준 뒤에
1과 연산을 해주면 값이 1이 나오기 때문에 비트마스크 추가를 할 수 있다
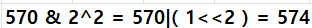
이 연산을 하게 되면

1을 넣을 수 있다.
값이 존재함을 비트마스크에 넣고싶다면
2진수로 바꾼뒤에 or 연산을 하면 된다
#비트마스크 Bit Mask 삭제
비트마스크 삭제인 경우에는
~연산을 해준 뒤에 & 연산을 함으로써 삭제를해준다
~를 해주면 값은 0이되고 그 외의 비트들은 1이 되므로
~를 해주고 & 연산을 해주면 인덱스를 삭제 할 수 있다
2번째 인덱스를 삭제 하고 싶은 경우에
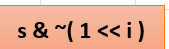
1을 <<연산을 2번 해주고 & 연산을 해준다


2번째 비트 의 값만 삭제할 수 있는 것을 알 수 있다.
#Exclusive OR 활용
Exclusive OR 는
값을 swap 하는데 사용 할 수 있는데
XOR 스왑 알고리즘은 두 변수를 임시 변수 없이 스왑하는 방법으로, XOR 연산을 사용합니다. 이는 메모리를 절약하고 코드의 간결성을 유지하는 데 유용합니다.
설명
XOR 연산
XOR (exclusive OR) 연산은 두 비트가 서로 다를 때 1을 반환하고, 같을 때 0을 반환합니다. 이를 통해 다음과 같은 성질을 이용할 수 있습니다:
- a ^ a = 0
- a ^ 0 = a
- a ^ b ^ b = a (교환 법칙과 결합 법칙에 따라)
XOR 스왑 알고리즘
- Step 1: x = x ^ y
- 이 단계에서 x는 x와 y의 XOR 값이 됩니다.
- 예: x = 5 (0101), y = 9 (1001) => x = 0101 ^ 1001 = 1100 (12)
- Step 2: y = x ^ y
- 이 단계에서 y는 x의 새로운 값(즉, x XOR y)과 y의 XOR 값이 되므로, 원래의 x 값을 얻습니다.
- 예: y = 1100 ^ 1001 = 0101 (5)
- Step 3: x = x ^ y
- 이 단계에서 x는 x의 새로운 값(즉, x XOR y)과 새로운 y의 XOR 값이 되므로, 원래의 y 값을 얻습니다.
- 예: x = 1100 ^ 0101 = 1001 (9)
매크로로
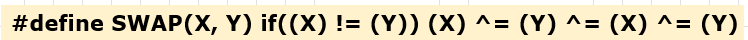
선언하여 쉽고 빠르게 사용 할 수 있다.
'[CS(Computer Science)] > 자료구조' 카테고리의 다른 글
| 그래프(자료구조) 대해서 알아보자 (0) | 2023.06.30 |
|---|