그래프:
(Graph)
자료구조의 일종으로 그래프는 연결되어 있는 원소 사이의 다대다 관계를 표현하는 자료구조이다.
정점(Node,Vertex) 간선(EDGE):정점간의 관계 로 표현된다
G =(V,E)로 나타낸다
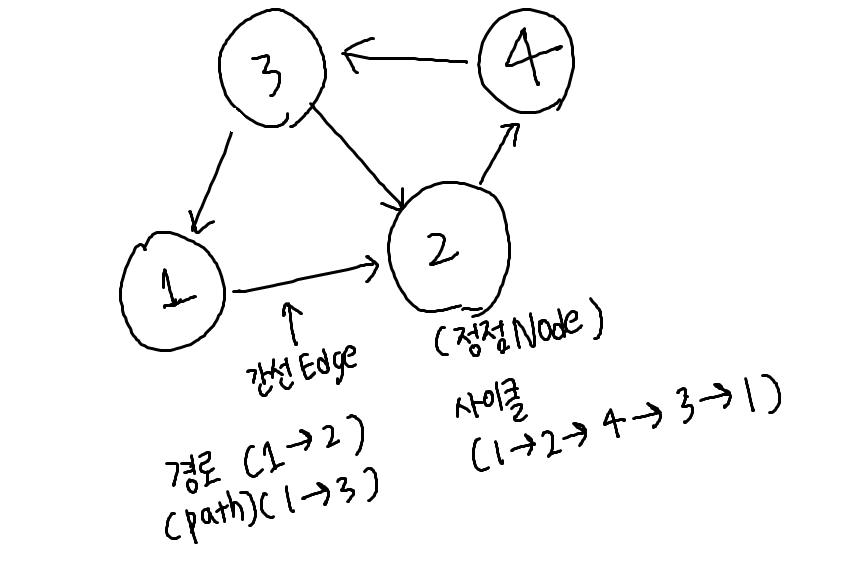
경로: 1에서2에서 가는경로, 1에서 3에서 가는 경로 등이 있다.
사이클 : 정점 1에서 다시 1로 돌아오는 경로
단순경로/단순사이클 : 경로/사이클에서 같은 정점을 두번 이상 방문하지 않는 경로/사이클
보통 말이 없으면 일반적으로 사용하는 경로와 사이클은 단순경로/사이클을 뜻한다
방향있는 그래프/ 방향없는 그래프
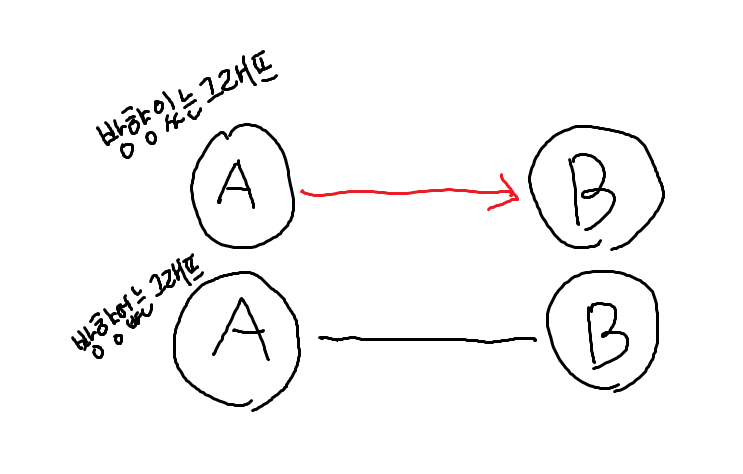
양방향 그래프 라고도 한다
루프: 간선의 양 끝점이 같은경우
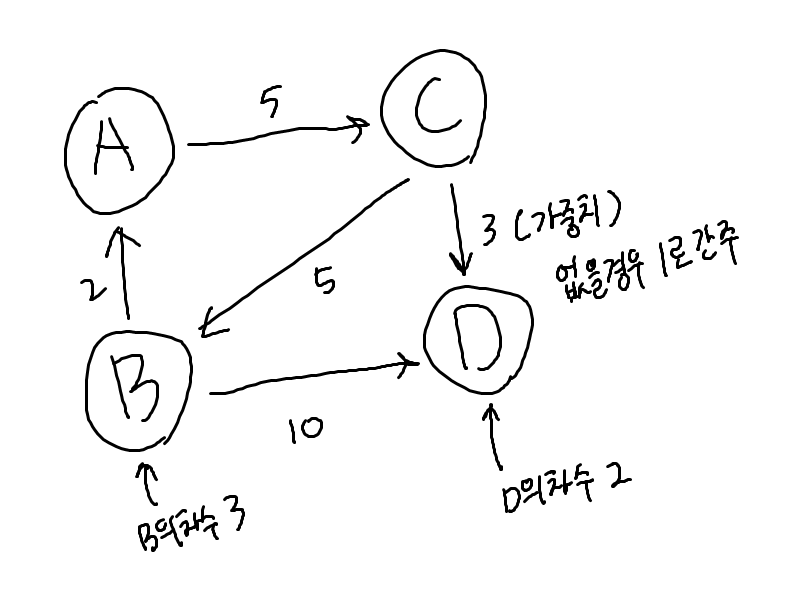
가중치: 있다면 A에서 B로 이동하는 거리 시간 비용 등등..
차수 : 정점과 연결되어 있는 간선의 개수
그래프의 표현 방법
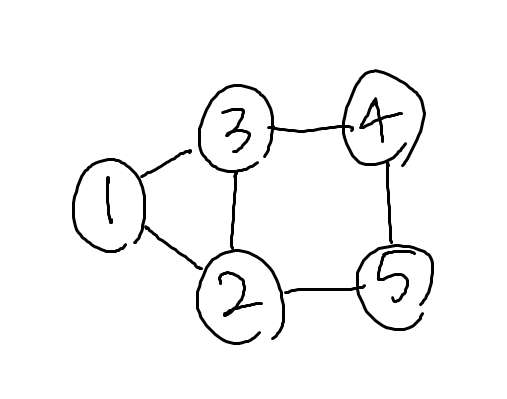
정점: {1,2,3,4,5}
간선: {(1,2),(1,3),(2,5),(2,3),(3,4),(4,5)}
그래프의 표현 방법에는 인접행렬과 인접 리스트를 활용한 방법 두가지가 있다.
인접 행렬을 사용한 경우
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 |
인접 리스트를 사용한 경우
(리스트는 동적으로 변경할 수 있어야 하고,연결 리스트나 동적으로 변경이 가능한 배열을 사용한다)
A[1] : 2 3
A[2]: 1 3 4
A[3]: 1 2 4
A[4]: 3 5
A[5]: 2 4
EX) 가중치가 있는 경우 A[2]: (2,3) (3,5) 등으로 가중치도 함께 저장
인접리스트 VS 인접 행렬
.인접 행렬은 정점 1000개의 그래프를 표현하기 위해서는 1000x1000의 행렬이 필요하고
인접 리스트는 1000개의 노드가 있으면 된다
만약에 이 그래프에 5개의 간선이 있다고 한다면
인접행렬은 1000x1000개 인접리스트는 1000(정점노드)+5(간선노드)개 의 노드가 필요하다
인접행렬의 공간복잡도는O(V^2)
인접리스트는 O(V+E) V는 정점 E는 간선의 개수
때문에 인접리스트는 희소 그래프를 표현하는데 적당하다
반면 1000개의 정점이있고 간선이 1000개인 경우 인접행렬로 구현하는게 더 효과적이면
이는 행렬의 접근성 때문이다 인접행렬은 인덱스를 사용하므로 O(1)으로 연결되었는지 확인 가능하지만
인접리스트는 헤드부터 노드를 찾을 때 까지 탐색을 진행해야 되므로 시간이 많이 걸린다
전자의 경우 희소 그래프 후자의 경우 밀집 그래프 이다
관련문제:
https://www.acmicpc.net/problem/13023
13023번: ABCDE
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
www.acmicpc.net
'[CS(Computer Science)] > 자료구조' 카테고리의 다른 글
| 비트마스크(BitMask) & 비트 연산(Bit Operator) 에 대해 알아보자 (0) | 2024.05.15 |
|---|
그래프:
(Graph)
자료구조의 일종으로 그래프는 연결되어 있는 원소 사이의 다대다 관계를 표현하는 자료구조이다.
정점(Node,Vertex) 간선(EDGE):정점간의 관계 로 표현된다
G =(V,E)로 나타낸다

경로: 1에서2에서 가는경로, 1에서 3에서 가는 경로 등이 있다.
사이클 : 정점 1에서 다시 1로 돌아오는 경로
단순경로/단순사이클 : 경로/사이클에서 같은 정점을 두번 이상 방문하지 않는 경로/사이클
보통 말이 없으면 일반적으로 사용하는 경로와 사이클은 단순경로/사이클을 뜻한다
방향있는 그래프/ 방향없는 그래프

양방향 그래프 라고도 한다
루프: 간선의 양 끝점이 같은경우

가중치: 있다면 A에서 B로 이동하는 거리 시간 비용 등등..
차수 : 정점과 연결되어 있는 간선의 개수
그래프의 표현 방법

정점: {1,2,3,4,5}
간선: {(1,2),(1,3),(2,5),(2,3),(3,4),(4,5)}
그래프의 표현 방법에는 인접행렬과 인접 리스트를 활용한 방법 두가지가 있다.
인접 행렬을 사용한 경우
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 |
인접 리스트를 사용한 경우
(리스트는 동적으로 변경할 수 있어야 하고,연결 리스트나 동적으로 변경이 가능한 배열을 사용한다)
A[1] : 2 3
A[2]: 1 3 4
A[3]: 1 2 4
A[4]: 3 5
A[5]: 2 4
EX) 가중치가 있는 경우 A[2]: (2,3) (3,5) 등으로 가중치도 함께 저장
인접리스트 VS 인접 행렬
.인접 행렬은 정점 1000개의 그래프를 표현하기 위해서는 1000x1000의 행렬이 필요하고
인접 리스트는 1000개의 노드가 있으면 된다
만약에 이 그래프에 5개의 간선이 있다고 한다면
인접행렬은 1000x1000개 인접리스트는 1000(정점노드)+5(간선노드)개 의 노드가 필요하다
인접행렬의 공간복잡도는O(V^2)
인접리스트는 O(V+E) V는 정점 E는 간선의 개수
때문에 인접리스트는 희소 그래프를 표현하는데 적당하다
반면 1000개의 정점이있고 간선이 1000개인 경우 인접행렬로 구현하는게 더 효과적이면
이는 행렬의 접근성 때문이다 인접행렬은 인덱스를 사용하므로 O(1)으로 연결되었는지 확인 가능하지만
인접리스트는 헤드부터 노드를 찾을 때 까지 탐색을 진행해야 되므로 시간이 많이 걸린다
전자의 경우 희소 그래프 후자의 경우 밀집 그래프 이다
관련문제:
https://www.acmicpc.net/problem/13023
13023번: ABCDE
문제의 조건에 맞는 A, B, C, D, E가 존재하면 1을 없으면 0을 출력한다.
www.acmicpc.net
'[CS(Computer Science)] > 자료구조' 카테고리의 다른 글
| 비트마스크(BitMask) & 비트 연산(Bit Operator) 에 대해 알아보자 (0) | 2024.05.15 |
|---|
