https://www.acmicpc.net/problem/7562
7562번: 나이트의 이동
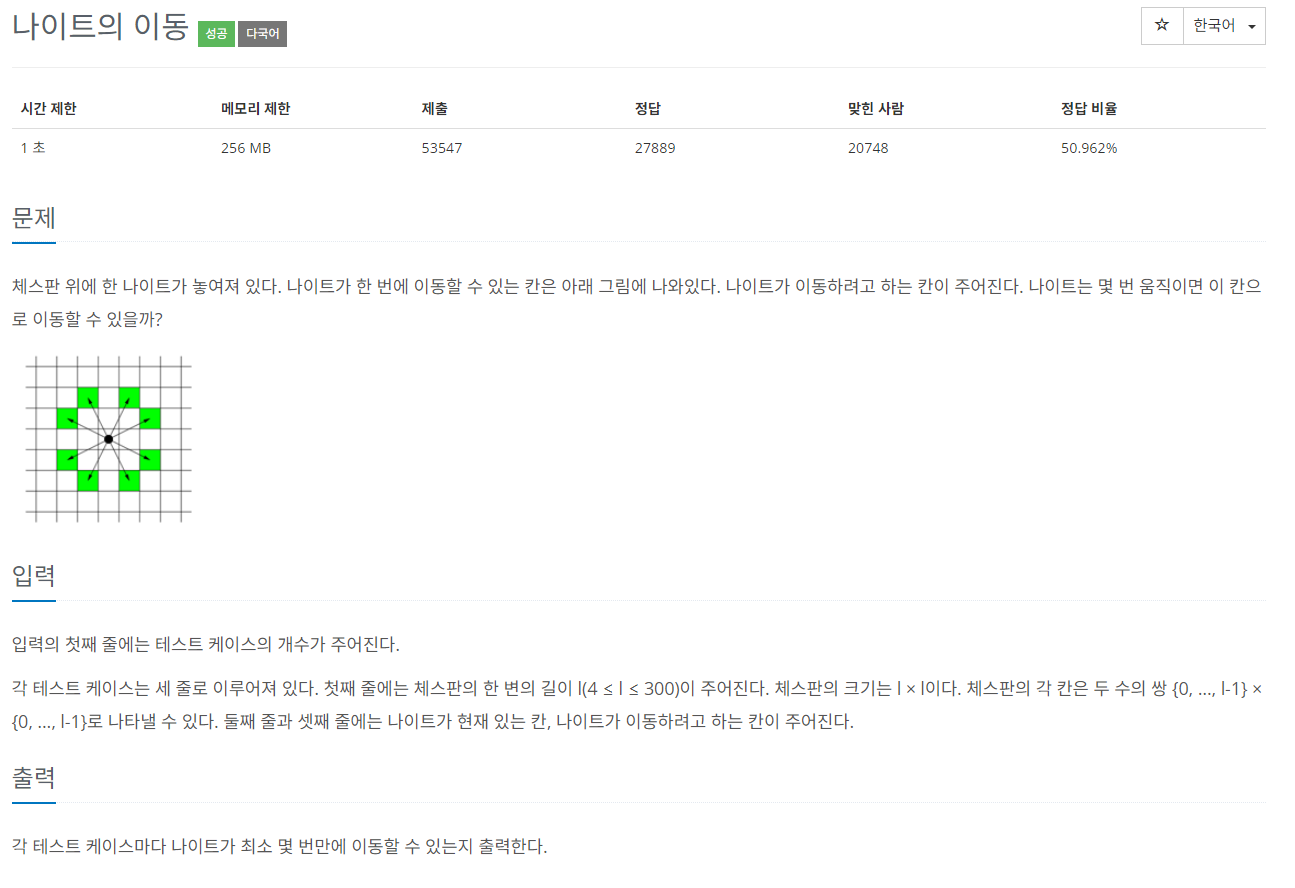
체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다. 나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수
www.acmicpc.net
#문제 간단 정리
체스판 위에서 나이트가 이동하는 최소 횟수를 계산하는 문제를 해결하기 위한 코드입니다. 코드는 입력으로 주어지는 테스트 케이스를 처리하고, 각 테스트 케이스에 대해 나이트가 최소 몇 번 움직여야 하는지를 출력합니다. 코드는 너비 우선 탐색(BFS)을 사용하여 문제를 해결합니다
#전체 코드
#include <iostream>
#include <queue>
using namespace std;
int dx[] = { 2, 1, -1, -2, -2 ,-1,1,2, };
int dy[] = { 1,2,2,1,-1,-2,-2,-1 };
struct point {
int x, y;
};
int main() {
int N; cin >> N;
while (N--) {
int I;
cin >> I;
point now, target;
cin >> now.x >> now.y >> target.x >> target.y;
if (now.x == target.x && now.y == target.y) {
cout << '0' << endl;
continue;
}
int chessBoard[300][300] = { 0, };
queue<point> q;
q.push(now);
chessBoard[q.front().x][q.front().y] = 0;
while (!q.empty()) {
int x = q.front().x;
int y = q.front().y;
q.pop();
for (int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if (0 <= nx && nx < I && 0 <= ny && ny < I) {
if (chessBoard[nx][ny] == 0) {
q.push({ nx,ny });
chessBoard[nx][ny] = chessBoard[x][y] + 1;
}
}
}
}
cout << chessBoard[target.x][target.y]<< endl;
}
return 0;
}
#문제 해결 방법
해당 문제는 나이트의 이동을 최소한의 움직임으로 목표 위치까지 가는 최단 거리를 찾는 문제입니다. 이를 위해 BFS(Breadth-First Search)를 사용합니다.
문제 해설:
- 나이트의 이동
나이트는 8가지 방향으로 움직일 수 있습니다. 문제에서 제시한 그림을 참고하면, 나이트의 모든 움직임을 (dx, dy)의 형태로 나타낼 수 있습니다. - BFS
BFS는 시작 지점부터 가장 가까운 지점들부터 차례대로 탐색하는 알고리즘입니다. 체스판에서의 나이트 이동도 이 알고리즘으로 효율적으로 해결할 수 있습니다. BFS를 사용하면, 각 칸에 도달하는 데 필요한 최소한의 움직임 횟수를 찾을 수 있습니다.
코드 설명:
- 변수
- dx, dy: 나이트의 이동 방향을 저장한 배열입니다.
- point: x, y 좌표를 갖는 구조체입니다.
- chessBoard: 각 위치에 도달하기 위한 최소 움직임 횟수를 저장하는 체스판입니다.
- 프로세스
- 테스트 케이스의 수를 입력 받습니다.
- 각 테스트 케이스마다
- 체스판의 크기, 시작 위치, 목표 위치를 입력 받습니다.
- 시작 위치와 목표 위치가 같다면, 움직일 필요가 없으므로 0을 출력하고 다음 테스트 케이스로 넘어갑니다.
- 그렇지 않다면, BFS로 최단 거리를 찾습니다.
- BFS를 진행하며, 체스판에 각 칸까지 도달하기 위한 최소 움직임 횟수를 저장합니다.
- 목표 위치까지의 최소 움직임 횟수를 출력합니다.
BFS를 사용하여 문제를 해결하면, 체스판의 각 칸까지 도달하는 데 필요한 최소 움직임 횟수를 효율적으로 찾을 수 있습니다.
'[백준] > C++' 카테고리의 다른 글
| 백준 13019번 A를 B로 [C++] (0) | 2023.09.17 |
|---|---|
| 백준 7576번 토마토 [C++] (0) | 2023.09.14 |
| 백준 1018번 체스판 다시 칠하기 [C++] (0) | 2023.09.06 |
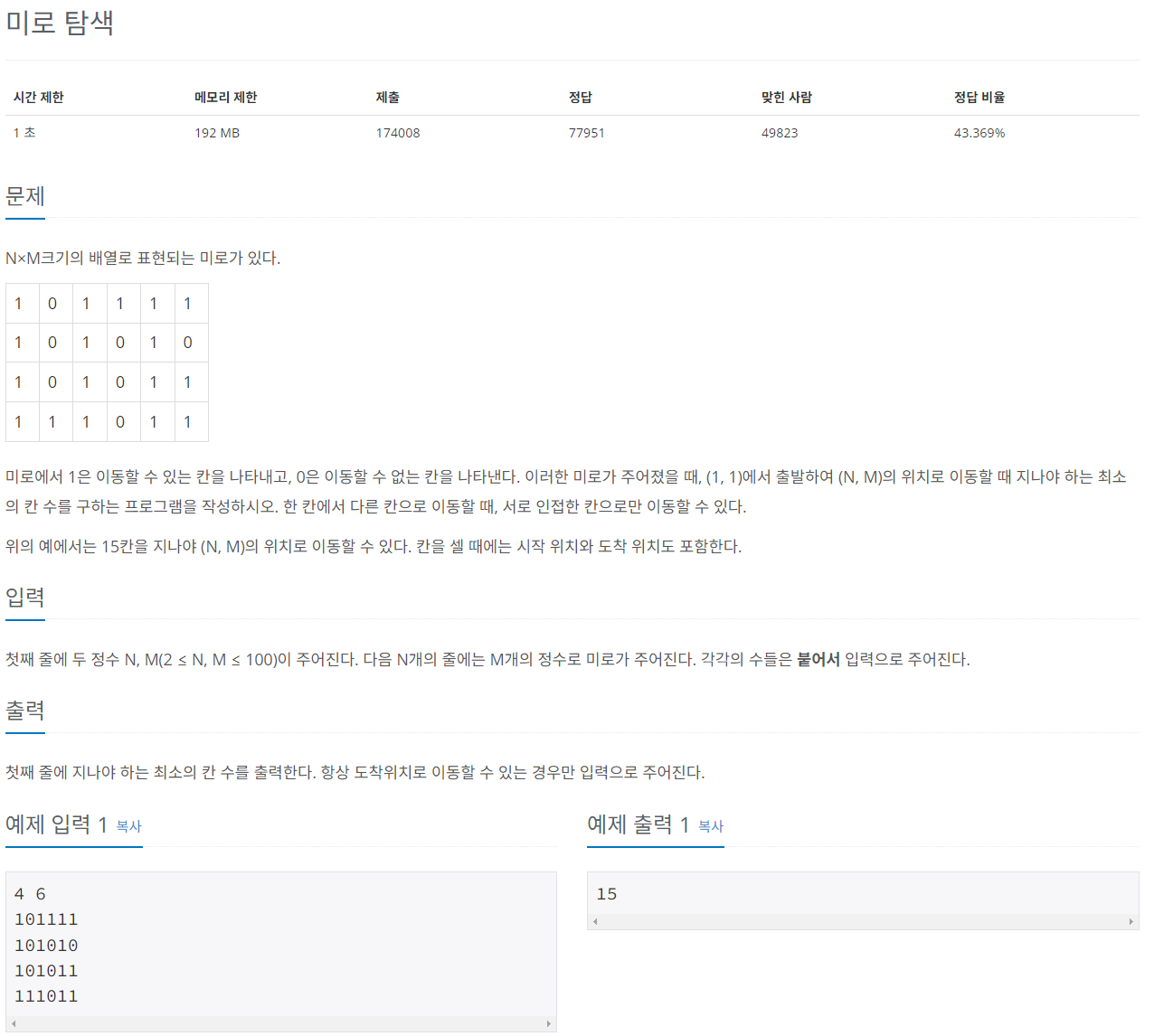
| 백준 2178번 미로 탐색[C++] (0) | 2023.09.06 |
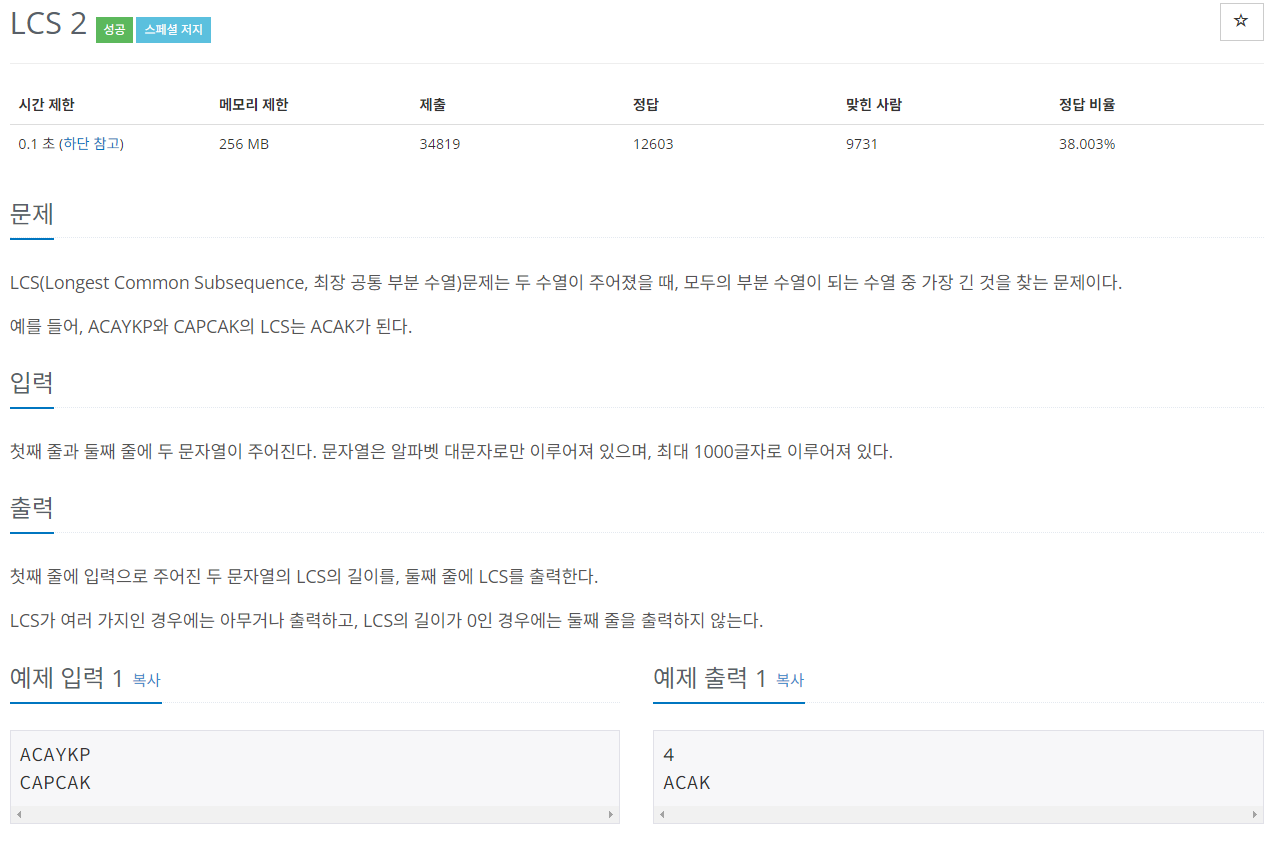
| 백준 9252번 LCS 2 [C++] (0) | 2023.09.03 |