경우없는 개발 블로그

https://www.acmicpc.net/problem/7579

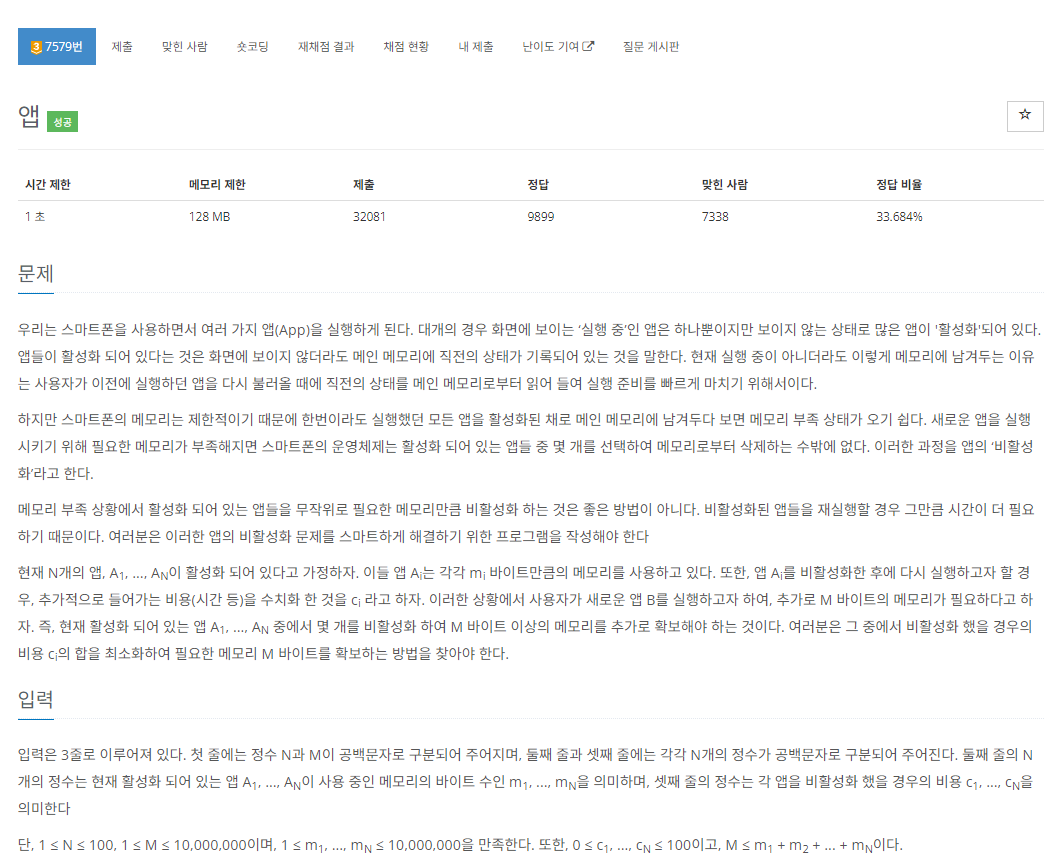
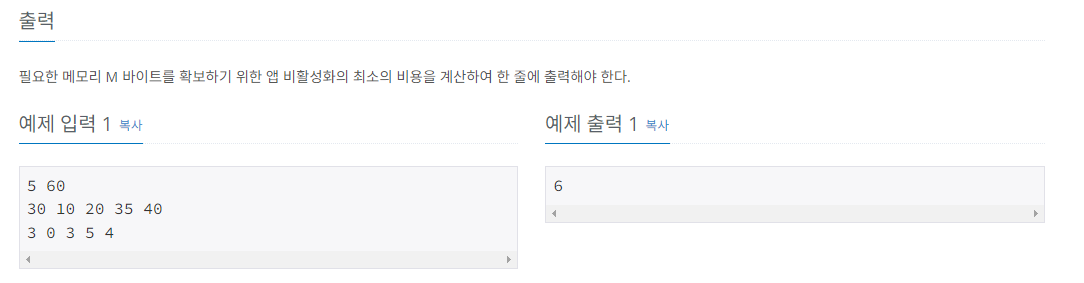
#문제 간단 정리

일단 배낭문제이다.

기존의 가방문제는 최소 무게를써서 최대 가치를 찾고

최대 가치를 가진 마지막 dp 배열이 정답이였다면

이 문제는 최소 비용으로 최대메모리를 찾고 그중에서 그 메모리이상의 첫번쨰 dp 배열을 찾는다는게 차이점

#문제 해결 방법

DP 배열을 dp[i][j]로 정의하고, 이를 "처음부터 i번째 앱까지 고려했을 때, 비활성화의 총 비용이 j일 때 확보할 수 있는 메모리의 최대량"으로 정의

즉 기존의 가방문제처럼 현재 비용(j)으로 구할수 있는 최대 메모리 dp[i][j]를 갱신한 후에

첫번째로 오는 M을 넘는 메모리를 가진 j(비용) 의 인덱스가 찾는 정답이다

쉽게 말하자면 dp 배열에는 순차적으로 j의 비용을 써서 얻는 최대 메모리가 저장되어있고

소비 j가 작으면서 M을 넘는 메모리의 허용량을 앞의 인덱스(작은j)부터 찾으면

즉 비용을 통해 최대 메모리를 가지도록 dp를 구현하고 최소 비용으로 목표 메리를 넘는 비용을 확인해 주면

된다는점이 기존 배낭문제랑 다르다.

#전체 코드

2차원 dp

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef long long ll;

int main() {
    ll N, M;
    cin >> N >> M;

    vector<ll> m(N), c(N);
    for (ll& memory : m) cin >> memory;
    for (ll& cost : c) cin >> cost;

    ll sumCost = 0; // 가능한 최대 비용의 합
    for (int i = 0; i < N; i++) sumCost += c[i];

    vector<vector<ll>> dp(N+1, vector<ll>(sumCost+1, 0));

    // DP를 이용해 해결
    for (int i = 1; i <= N; i++) {
        for (int j = 0; j <= sumCost; j++) {
            // 현재 앱 i를 비활성화하지 않는 경우
            dp[i][j] = dp[i-1][j];
            // 현재 앱 i를 비활성화할 수 있고, 그러기 위한 비용이 충분한 경우
            if (j >= c[i-1]) {
                dp[i][j] = max(dp[i][j], dp[i-1][j-c[i-1]] + m[i-1]);
            }
        }
    }

    // 필요한 메모리 M 바이트를 확보하기 위한 최소 비용 찾기
    ll answer = sumCost;
    for (int j = 0; j <= sumCost; j++) {
        if (dp[N][j] >= M) {
            answer = j;
            break;
        }
    }

    cout << answer << endl;

    return 0;
}

1차원dp

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

typedef long long ll;

int main() {
    ll N, M;
    cin >> N >> M;

    vector<ll> memory(N), cost(N);

    for (int i = 0; i < N; i++) {
        cin >> memory[i];
    }
    for (int i = 0; i < N; i++) {
        cin >> cost[i];
    }

    ll maxCost = 100 * N; // 최대 비용
    vector<ll> dp(maxCost+1, 0); // 비용에 따른 메모리 최대치 저장

    for (int i = 0; i < N; i++) {
        for (int j = maxCost; j >= cost[i]; j--) {
            dp[j] = max(dp[j], dp[j-cost[i]] + memory[i]);
        }
    }

    // 필요한 메모리 M 바이트를 확보하기 위한 최소 비용을 찾기
    ll answer = maxCost;
    for (int i = 0; i <= maxCost; i++) {
        if (dp[i] >= M) {
            answer = i;
            break;
        }
    }

    cout << answer << endl;

    return 0;
}

https://www.acmicpc.net/problem/2644

#문제 간단 정리

dfs 혹은 bfs를 사용하자

#문제 해결 방법

dfs를 사용해서 depth를 반환하도록 해줬다.

근데 만들고 나니     result = min(result, curResult); 로 최소 거리를 확인해 줘야 되서

bfs 로 풀면 더 쉽게 풀거라는 생각이 들었따.

#전체 코드

dfs 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

bool check[103];

int dfs(int node, vector<vector<int>>& families, int depth, int target) {
    if (node == target) {
        return depth;
    }
    check[node] = true;

    int result = INT_MAX;
    for (int i = 0; i < families[node].size(); i++) {
        int next = families[node][i];
        if (!check[next]) {
            int curResult = dfs(next, families, depth + 1, target);
            if (curResult != -1) {
                result = min(result, curResult);
            }
        }
    }

    return result == INT_MAX ? -1 : result;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin >> N;

    int start, target;
    cin >> start >> target;

    vector<vector<int>> families(N + 1);

    int m;
    cin >> m;
    for (int i = 0; i < m; i++) {
        int x, y;
        cin >> x >> y;

        families[x].push_back(y);
        families[y].push_back(x);
    }

    fill_n(check, 103, false);
    int result = dfs(start, families, 0, target); 

    cout << result << '\n';

    return 0;
}

bfs 코드

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int bfs(int start, int target, vector<vector<int>>& families) {
    vector<bool> visited(families.size(), false);
    queue<pair<int, int>> q; // {노드 번호, 촌수}

    q.push({start, 0}); // 시작 노드와 촌수 0부터 시작
    visited[start] = true;

    while (!q.empty()) {
        int current = q.front().first;
        int distance = q.front().second;
        q.pop();

        if (current == target) {
            return distance;
        }

        for (int next : families[current]) {
            if (!visited[next]) {
                visited[next] = true;
                q.push({next, distance + 1});
            }
        }
    }

    return -1; // 목표 노드에 도달할 수 없는 경우
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin >> N;

    int start, target;
    cin >> start >> target;

    vector<vector<int>> families(N+1);

    int m;
    cin >> m;
    for (int i = 0; i < m; i++) {
        int x, y;
        cin >> x >> y;

        families[x].push_back(y);
        families[y].push_back(x);
    }

    int result = bfs(start, target, families);

    cout << result << '\n';

    return 0;
}

https://www.acmicpc.net/problem/2473

#문제 간단 정리

이전의 두 용액 문제와 같이 

두 포인터를 사용한 문제

#문제 해결 방법

이전의 두 용액에서와는 달리

첫번째 용액을 고르고 

두번째와 세번째를 두 포인터로 좌 우를 조절하며 가장 0과 가까운 용액을 찾는다.

그리고.. 그냥 첫번째와 두번째 용액을 브루트 포스로 전부 탐색하고

세번 째 용액을 이진탐색으로 고르는 방법이 있다.

이게 좀 더 복잡하다.

#전체 코드

1번 코드 (두 포인터)

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

typedef long long ll;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin >> N;  // N의 값을 입력받습니다.

    vector<ll> liquids(N);

    for (int i = 0; i < N; i++) {
        cin >> liquids[i];
    }

    sort(liquids.begin(), liquids.end());

    ll closestSum = LLONG_MAX;
    int trueAnswers[3] = { -1, -1, -1 };

    // 첫 번째 용액을 고정합니다.
    for (int i = 0; i < N - 2; i++) {
        int left = i + 1;
        int right = N - 1;
        
        // 두 번째와 세 번째 용액을 탐색합니다.
        while (left < right) {
            ll sum = liquids[i] + liquids[left] + liquids[right];
            if (abs(sum) < abs(closestSum)) {
                closestSum = abs(sum);  // 최소 합을 업데이트합니다.
                trueAnswers[0] = liquids[i];
                trueAnswers[1] = liquids[left];
                trueAnswers[2] = liquids[right];
            }
            
            // 합을 조절하여 0에 더 가까운 조합을 찾습니다.
            if (sum > 0) {
                right--;
            } else {
                left++;
            }
        }
    }

    cout << trueAnswers[0] << " " << trueAnswers[1] << " " << trueAnswers[2] << '\n';
    return 0;
}

2번코드 (이진탐색)

#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;

typedef long long ll;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N;
    cin >> N;
    vector<ll> liquids(N);

    for (int i = 0; i < N; i++) {
        cin >> liquids[i];
    }

    sort(liquids.begin(), liquids.end());

    ll closestSum = LLONG_MAX;
    int resA = 0, resB = 0, resC = 0;

    for (int i = 0; i < N; ++i) {
        for (int j = i + 1; j < N; ++j) {
            int left = j + 1, right = N - 1;

            while (left <= right) {
                int mid = left + (right - left) / 2;
                ll sum = liquids[i] + liquids[j] + liquids[mid];

                if (abs(0 - sum) < closestSum) {
                    closestSum = abs(0 - sum);
                    resA = i, resB = j, resC = mid;
                }

                if (sum > 0) right = mid - 1;
                else if (sum < 0) left = mid + 1;
                else break; // sum이 0인 경우, 최적의 조합을 찾음
            }
        }
    }

    cout << liquids[resA] << " " << liquids[resB] << " " << liquids[resC] << '\n';
    return 0;
}

https://www.acmicpc.net/problem/1806

#문제 간단 정리

투 포인터를 활용하는 문제

많이 볼 수 있는 유형이라 많이 접근해봤다면 쉽게 풀 수 있다

#문제 해결 방법

우선 브루트 포스를 사용하면 

시간 초과가 날 것이 자명하기 때문에

값보다 작다면 end포인터를 ++ 하면서 길이를 늘리고

값보다 크다면 start 포인터를 -- 하면서 최소 길이를 확인합니다.

이는 가장 '짧은' 연속 부분합 길이를 찾는다고 문제에 나와있기 때문에

투 포인터를 사용해 조절해가며 길이를 찾는다는 아이디어를 생각 할 수 있습니다.

#전체 코드

#include <iostream>
#include <vector>
#include <climits>

using namespace std;

int main()
{
    int N, M;
    cin >> N >> M;
    vector<int> nums(N);
    for (int i = 0; i < N; i++) {
        cin >> nums[i];
    }

    int end = 0, start = 0,sum = 0;
    int minlength = INT_MAX;

    while (end < N) {

        if (sum < M) {
            sum += nums[end++];
        }
        while(sum >= M) {
            minlength = min(minlength, end - start);
            sum -= nums[start++];

        }
    }

    if (minlength == INT_MAX) minlength = 0;

    cout << minlength << '\n';
}

https://www.acmicpc.net/problem/20040

#문제 간단 정리

사이클이 언제 생성되는지 출력하는 문제

즉 사이클을 확인할 수 있는 유니온 파인드 (Union-Find)를 알고 있는지 물어보는 문제다

그렇기 때문에 유니온 파인드를 구현하자

#문제 해결 방법

유니온 파인드 동작 방식

유니온 파인드에서는 각 노드가 하나의 그룹을 나타내고, 각 그룹은 트리 구조로 구성됩니다. 트리의 루트 노드는 그 그룹을 대표합니다. 초기 상태에서는 각 노드가 자기 자신만을 포함하는 독립적인 그룹을 형성합니다.

1. Find 연산: 특정 노드가 속한 그룹의 대표(루트 노드)를 찾습니다. 노드가 속한 트리의 루트 노드를 찾아 그룹을 식별할 수 있습니다.
2. Union 연산: 두 개의 노드가 주어졌을 때, 이 노드들을 포함하는 두 그룹을 하나로 합칩니다. 이는 두 트리의 루트 노드를 연결하여 수행됩니다.

사이클 게임 문제 해결 방법

사이클 게임에서는 점들이 주어지고, 차례대로 점들을 연결하는 선분을 그립니다. 사이클이 형성되는 순간 게임이 종료됩니다. 사이클이란, 선분들이 연결되어 처음 시작한 점으로 돌아올 수 있는 경로를 의미합니다.

문제를 풀 때 유니온 파인드를 사용하는 이유는 각 선분을 그릴 때마다 두 점이 이미 같은 그룹에 속해 있는지(Find)를 확인하고, 속하지 않는 경우 두 점을 연결하는 그룹을 하나로 합치기(Union) 위함입니다.

1. 초기 상태: 모든 점은 자기 자신만을 포함하는 독립적인 그룹을 형성합니다.
2. 선분을 그릴 때마다: 주어진 두 점에 대해 Find 연산을 수행하여, 두 점이 이미 같은 그룹에 속해 있는지 확인합니다.
   • 같은 그룹에 속해 있지 않다면: 이는 아직 사이클이 형성되지 않았음을 의미합니다. 이 경우, 두 점을 연결하는 Union 연산을 수행하여 두 그룹을 합칩니다.
   • 같은 그룹에 속해 있다면: 두 점을 연결하는 순간 사이큀이 형성됩니다. 왜냐하면 이미 같은 그룹에 속해 있다는 것은 이전에 이 두 점을 경유하는 경로가 이미 존재한다는 것을 의미하며, 두 점을 다시 연결하면 사이클이 완성되기 때문입니다.
3. 사이클 형성 여부: 만약 같은 그룹에 속해 있다는 것이 확인되면, 그 순간이 바로 사이클이 처음으로 형성된 차례입니다.

#전체 코드

#include <iostream>
#include <vector>
using namespace std;

#define MAX 500000

int parent[MAX]; // 부모 노드를 저장하는 배열

int Find(int x) {
    if (parent[x] == x)
        return x;
    return parent[x] = Find(parent[x]); // 경로 압축
}

void Union(int x, int y) { // 함수 이름을 `Union`으로 변경
    x = Find(x);
    y = Find(y);

    if (x != y) {
        if (x < y)
            parent[y] = x;
        else
            parent[x] = y;
    }
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    
    int n, m;
    cin >> n >> m;

    for (int i = 0; i < n; i++) {
        parent[i] = i; // 각 노드의 부모를 자기 자신으로 초기화
    }

    for (int i = 1; i <= m; i++) {
        int a, b;
        cin >> a >> b;

        // 이미 같은 집합에 속해 있다면, 사이클이 형성됨
        if (Find(a) == Find(b)) {
            cout << i; // 사이클이 처음으로 만들어진 차례의 번호 출력
            return 0;
        }

        Union(a, b); // 두 노드를 하나의 집합으로 합치기
    }

    cout << "0"; // 모든 차례를 처리한 후에도 사이클이 형성되지 않았다면 0 출력
    return 0;
}

https://www.acmicpc.net/problem/2550

#문제 간단 정리

#문제 해결 방법

1. 문제 이해하기

• 스위치와 전구가 있고, 각 스위치는 특정 전구를 켭니다.
• 스위치들을 함께 누르면, 그들의 연결선이 교차하지 않는 경우에만 전구들이 켜집니다.
• 우리의 목표는 최대한 많은 전구를 켜는 것입니다.
• 여기서 우리는 스위치의 순서대로 전구를 순서대로 나열했을때 가장 긴 증가는 부분수열을 구하면 가장 많이 킬 수 있는 전구의 개수를 알 수 있다는걸 파악 할 수 있습니다.(LIS)

2. 전구와 스위치 연결 관계 파악하기

• 각 전구가 몇 번째 스위치에 연결되어 있는지를 파악합니다. 이는 우리가 스위치를 눌렀을 때 어떤 전구가 켜지는지 알기 위함입니다.

3. 최장 증가 부분 수열(LIS) 개념 이해하기

• LIS는 주어진 순열에서 어떤 원소들을 선택했을 때, 선택된 원소들이 증가 순서를 유지하는 가장 긴 부분 순열을 의미합니다.
• 이 문제에서는 스위치와 전구의 연결선이 교차하지 않기 위해 LIS를 찾아야 합니다.

4. 문제 해결을 위한 동적 프로그래밍(DP) 사용하기

• DP를 사용해 각 스위치까지 고려할 때, 교차하지 않고 켤 수 있는 최대 전구 수를 찾습니다.
• 각 스위치에 대해, 그 스위치를 포함하는 최장 증가 부분 수열의 길이를 저장합니다.
• 이 과정에서, 각 스위치의 이전 스위치들과 비교하여, 연결선이 교차하지 않고 증가 순서를 만족하는 가장 긴 수열을 찾습니다.

5. 최장 증가 부분 수열 역추적하기

• DP를 통해 LIS의 길이를 찾은 후, 그 수열을 구성하는 스위치들을 역추적합니다.
• 역추적을 통해 어떤 스위치들을 눌러야 최대한 많은 전구를 켤 수 있는지를 파악합니다.

6. 결과 정리 및 출력하기

• 역추적한 스위치들을 오름차순으로 정렬합니다.
• 정렬된 스위치들을 출력하여, 눌러야 하는 스위치의 번호를 보여줍니다.

결론

• 이 문제는 스위치와 전구의 연결 관계를 분석하여, 전선이 교차하지 않는 방식으로 최대한 많은 전구를 켜는 스위치 조합을 찾는 것입니다.
• 동적 프로그래밍을 사용하여 각 스위치별로 교차하지 않고 켤 수 있는 최대 전구의 수를 계산하고, 최장 증가 부분 수열을 찾아 역추적하는 과정을 거쳐 최적의 스위치 조합을 결정합니다.
• 최종적으로, 이러한 스위치 조합을 오름차순으로 정렬하여 출력함으로써, 문제의 해결책을 제시합니다.

최장 증가 부분 수열(LIS) 문제에서의 DP

LIS 문제에서 우리는 주어진 시퀀스에서 가장 긴 증가하는 부분 수열을 찾아야 합니다. 이를 위해 DP를 사용하여 각 위치에 대해 최장 증가 부분 수열의 길이를 계산합니다.

DP 접근 방식:

1. 초기화: 길이가 N인 입력 시퀀스에 대해, 길이 N의 dp 배열을 생성하고 모든 요소를 1로 초기화합니다. dp[i]는 i번째 원소를 마지막으로 하는 최장 증가 부분 수열의 길이를 저장합니다. 초기값 1은 각 원소가 자신만으로 구성된 부분 수열을 의미합니다.
2. 부분 문제 해결: i번째 원소에 대해, 0부터 i-1까지의 모든 j에 대해 다음을 수행합니다:
   • 만약 j번째 원소가 i번째 원소보다 작다면(arr[j] < arr[i]), j번째 원소를 포함하는 부분 수열에 i번째 원소를 추가할 수 있습니다. 이 경우, dp[i]는 dp[j] + 1과 현재 dp[i] 값 중 더 큰 값으로 업데이트됩니다. 이는 i번째 원소를 포함하여 얻을 수 있는 최장 증가 부분 수열의 길이를 의미합니다.
3. 전체 문제 해결: 모든 i에 대해 위의 과정을 수행한 후, dp 배열에 저장된 값들 중 최댓값이 전체 시퀀스의 최장 증가 부분 수열의 길이가 됩니다.

#전체 코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    int N;
    cin >> N;

    vector<int> switches(N+1), bulbs(N+1), positions(N+1), dp(N+1), prev(N+1);
    for (int i = 1; i <= N; ++i) {
        cin >> switches[i];
    }
    for (int i = 1; i <= N; ++i) {
        int bulb;
        cin >> bulb;
        positions[bulb] = i;
    }
    for (int i = 1; i <= N; ++i) {
        bulbs[i] = positions[switches[i]];
    }

    fill(dp.begin(), dp.end(), 1);
    int maxLen = 0, lastIndex = 0;
    for (int i = 1; i <= N; ++i) {
        prev[i] = -1;
        for (int j = 1; j < i; ++j) {
            if (bulbs[j] < bulbs[i] && dp[j] + 1 > dp[i]) {
                dp[i] = dp[j] + 1;
                prev[i] = j;
            }
        }
        if (dp[i] > maxLen) {
            maxLen = dp[i];
            lastIndex = i;
        }
    }

    cout << maxLen << endl;

    vector<int> sequence;
    while (lastIndex != -1) {
        sequence.push_back(switches[lastIndex]);
        lastIndex = prev[lastIndex];
    }

    sort(sequence.begin(), sequence.end());
    for (int i = 0; i < sequence.size(); ++i) {
        cout << sequence[i] << " ";
    }

    return 0;
}

https://www.acmicpc.net/problem/1197

#문제 간단 정리

최소 스패닝 트리를 구현하는되는 문제

즉 크루스칼 알고리즘이랑 

프림 알고리즘을 구현하면 되는 문제이다

https://yabmoons.tistory.com/191

이 블로그에 크루스칼이 잘 정리 되어있으니까 모른다면 참고하면 좋을 것 같다. 

#문제 해결 방법

유니온 파인드를 우선 구현하고 그 이후에 

크루스칼을 구현하면 된다.

#전체 코드

#include <iostream>
#include <cstring> 
#include <climits>
#include <algorithm>
#include <vector>
using namespace std;

#define MAX 10001


int Parent[MAX];

vector<pair<int, pair<int, int>>> V;

int Find(int x) {
    if (Parent[x] == x) return x;
    else return Parent[x] = Find(Parent[x]);
}

void Union(int x, int y) {
    x = Find(x);
    y = Find(y);

    if (x != y) Parent[y] = x;
}

bool SameParent(int x, int y) {
    x = Find(x);
    y = Find(y);

    if (x == y) return true;
    else return false;
}

int main() {
    
    int Vertex, E, Answer=0;

    cin >> Vertex >> E;
    for (int i = 0; i < E; i++) {
        int From, To, Cost;
        cin >> From >> To >> Cost;

        V.push_back(make_pair(Cost, make_pair( From,To )));
    }

    sort(V.begin(), V.end());

    for (int i = 1; i <= Vertex; i++) {
        Parent[i] = i;
    }

    for (int i = 0; i < E; i++) {
        if (SameParent(V[i].second.first, V[i].second.second) == false) {
            Union(V[i].second.first, V[i].second.second);
            Answer = Answer + V[i].first;
        }
    }

    cout << Answer << '\n';

    return 0;
}

https://www.acmicpc.net/problem/16139

#문제 해결 방법

우선 시간제한을 확인했을때 

매번 매 쿼리마다 구간을 전부 확인하면 시간초과가 난다.

알파벳이 나오는 순서가 고정되어있기 때문에

나는 문자열의 길이와 알파벳의 개수만큼의 크기를 가지는 2차원 배열을 선언해서

예 : [string.size()][26] 

문자열의 알파벳 인덱스에 해당하는 열에 카운팅을 해줫다.

[index][알파벳-'a'] +=1 

누적합이기 때문에

r에서 l-1  의 해당하는 알파벳 인덱스를 빼주면

int count = alphaCount[r][alpha - 'a'];
        if (l > 0) {
            count -= alphaCount[l - 1][alpha - 'a'];
        }

구간에서의 나온 알파벳 나온 횟수를 알 수 있다..

는데 기본적인 누적합 원리이다.

설명이 이해가 안된다면 누적합에 대해서 한번 살펴본뒤에

코드를 보면 이해 될 것이다.

#전체 코드

#include <iostream>
#include <vector>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    string s;
    cin >> s;

    vector<vector<int>> alphaCount(s.size(), vector<int>(26, 0));

    alphaCount[0][s[0] - 'a'] = 1;

    for (int i = 1; i < s.size(); i++) {
        for (int j = 0; j < 26; j++) {
            alphaCount[i][j] = alphaCount[i - 1][j];
        }
        alphaCount[i][s[i] - 'a'] += 1;
    }

    int q;
    cin >> q;
    while (q--) {
        char alpha;
        int l, r;
        cin >> alpha >> l >> r;

        int count = alphaCount[r][alpha - 'a'];
        if (l > 0) {
            count -= alphaCount[l - 1][alpha - 'a'];
        }

        cout << count << '\n';
    }

    return 0;
}

https://www.acmicpc.net/problem/1012

#문제 간단 정리

#문제 해결 방법

그래프를 이용한 탐색 구현 문제이다.

주요 로직은 양배추가 있는 x y 좌표들만 따로 저장해서

양배추들 좌표들만 따로 순회를 해주는데

만약 이전에 접근한 적이 없다면 

counting 전역변수로 새로운 진입을 카운팅 해준다.

여러모로 전역변수를 쓰면 편하다

#전체 코드

#include <iostream>
#include <vector>
using namespace std;

int M, N, K;
int counting;

int dx[4] = { 1,0,-1,0 };
int dy[4] = { 0,1,0,-1 };

void dfs(vector<vector<int>> &map, vector<vector<bool>> &check ,int x, int y) {
    
    check[x][y] = true;
    for (int i = 0; i < 4; i++) {
        int nx = x + dx[i];
        int ny = y + dy[i];

        if (nx >= 0 && nx < M && ny >= 0 && ny < N) {
            if (map[nx][ny] == 1 && check[nx][ny] == false) {
                dfs(map, check, nx, ny);
            }
        }

    }

}

int main() {
    

    int T;
    cin >> T;

    while (T--) {
        counting = 0;
        cin >> M >> N >> K;
        vector<vector<int>> map(M, vector<int>(N, 0));
        vector<vector<bool>> check(M, vector<bool>(N, false));
        vector<pair<int, int>> cabbages;

        for (int i = 0; i < K; i++) {
            int x, y;
            cin >> x >> y;

            map[x][y] = 1;
            cabbages.push_back({ x,y });
        }

        for (pair<int, int> a : cabbages) {
            if (check[a.first][a.second] == false) {
                counting++;
                dfs(map, check, a.first, a.second);
            }
        }
        cout << counting << '\n';
    }



    return 0;
}

https://www.acmicpc.net/problem/2615

#문제 간단 정리

#문제 해결 방법

가장 주의해야될 점이 연속된5개의 돌을 확인해서 승리로 판단할 수 있지만, 만약 

뒤쪽 방향도 확인하지 않는다면 육목임에도 중간부터 확인해서 오목으로 오판해서

승리로 간주할 수 있다.

때문에 뒤쪽도 확인한 뒤에 뒤의 인덱스로 업데이트 하는 기능을 신경 써 줘야 한다

#전체 코드

#include <iostream>
#include <vector>
using namespace std;

const int N = 19;
int board[N][N];
int backwardX, backwardY;

// 방향을 나타내는 배열 (가로, 세로, 대각선 오른쪽 위, 대각선 오른쪽 아래)
int dx[] = { 0, 1, 1, -1 };
int dy[] = { 1, 0, 1, 1 };

bool isValid(int x, int y) {
    return x >= 0 && x < N&& y >= 0 && y < N;
}

bool checkFive(int row, int col) {
    if (board[row][col] == 0) return false; // 빈 칸은 검사할 필요 없음

    for (int dir = 0; dir < 4; dir++) {
        int count = 1;
        // 앞쪽 방향으로 연속된 돌 확인
        int x = row + dx[dir];
        int y = col + dy[dir];
        while (isValid(x, y) && board[x][y] == board[row][col]) {
            count++;
            x += dx[dir];
            y += dy[dir];
        }

        // 연속된 돌의 앞쪽 끝 검사
        int forwardX = x;
        int forwardY = y;

        // 반대 방향으로 연속된 돌 확인
        x = row - dx[dir];
        y = col - dy[dir];
        while (isValid(x, y) && board[x][y] == board[row][col]) {
            count++;
            x -= dx[dir];
            y -= dy[dir];
        }

        // 연속된 돌의 뒤쪽 끝 검사
        backwardX = x +dx[dir];
        backwardY = y +dy[dir];

        // 정확히 5개의 돌이 연속되는지 확인
        if (count == 5) {
            // 양 끝이 둘 다 유효하지 않거나, 양쪽 끝에 동일한 색의 돌이 없는 경우에만 true 반환
            if ((!isValid(forwardX, forwardY) || board[forwardX][forwardY] != board[row][col]) &&
                (!isValid(backwardX -dx[dir], backwardY -dy[dir]) || board[backwardX -dx[dir]][backwardY- dy[dir]] != board[row][col])) {
                return true;
            }
        }
    }
    return false;
}

int main() {
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cin >> board[i][j];
        }
    }

    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (checkFive(i, j)) {
                cout << board[i][j] << "\n" << backwardX + 1 << " " << backwardY + 1 << endl;
                return 0;
            }
        }
    }

    cout << 0 << '\n'; // 승자 없음
    return 0;
}