[백준]/C++
백준 28333번 화이트 칼라 [C++]
경우42
2025. 3. 18. 12:34
반응형
https://www.acmicpc.net/problem/28333


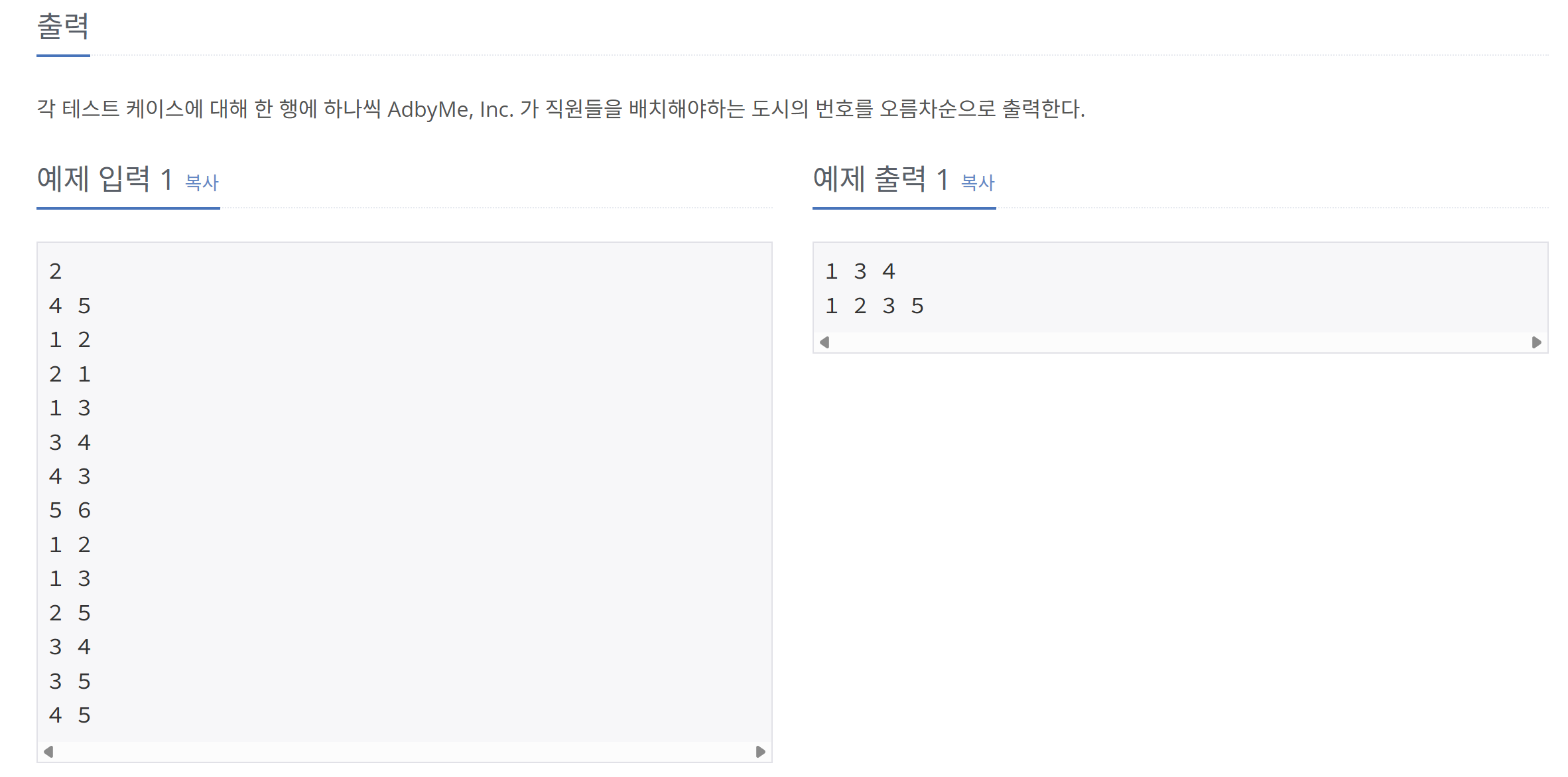
#문제 간단 정리
역방향 bfs 문제
#문제 해결 방법
여러개의 최단경로의
경로상의 도시들을 선택하는 문제
역방향 bfs에 대한 아이디어가 없었기에
최단경로로 다익스트라를 선택해서
다익스트라가 경로를
기억하도록 변경해서 했더니
최단경로가 여러개가 될 수 있다는 것을 간과했다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <climits>
#include <cstring>
using namespace std;
int dist[1001];
vector<vector<int>> nodes;
vector<int> routes;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
while (t--) {
nodes.clear();
nodes.resize(1001);
fill(dist, dist + 1001, 123456789);
routes.clear();
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
nodes[a].push_back(b);
}
//dijkstra 현재거리 , 현재노드, 경로
priority_queue<pair<int, pair<int, vector<int>>>> pq;
pq.push({ 0, {1, {1}} });
dist[1] = 0;
while (!pq.empty()) {
int curDist = -pq.top().first;
int curNode = pq.top().second.first;
vector<int> curPath = pq.top().second.second;
pq.pop();
if (dist[curNode]< curDist) continue;
for (int i = 0; i < nodes[curNode].size(); i++) {
int nextNode = nodes[curNode][i];
int nextDist = curDist + 1;
if (dist[nextNode] > nextDist) {
dist[nextNode] = nextDist;
vector<int> nextPath = curPath;
nextPath.push_back(nextNode);
if (nextNode == n) routes = nextPath;
pq.push({ -nextDist, {nextNode, nextPath} });
}
}
}
for (auto a : routes) {
cout << a << "";
}
cout << "\n";
}
return 0;
}
그래서 이 아이디어는 틀리고
거리가 1이기 때문에
bfs로 쉽게 최단경로를 탐색 가능하다.
이때 각각의 노드에 최단경로를 기록하고
역방향으로 최단경로를 갱신하면서
i 번째 노드를 갱신하고 있다면
i 번째의 역방향 거리 + i 번째의 순방향 거리를 더해서
D = 1부터 n까지의 최단거리 가 나오게 되면
그 노드가 최단경로에 포함되는 노드인걸 확인 가능하다
dist1 = 순방향 최단경로 배열
dist2 = 역방향 최단경로 배열

#전체 코드
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = 1e9;
// BFS 함수: start에서 시작하여 graph를 따라 각 노드까지의 최단 거리를 계산합니다.
void bfs(int start, const vector<vector<int>>& graph, vector<int>& dist) {
queue<int> q;
dist[start] = 0;
q.push(start);
while (!q.empty()) {
int cur = q.front();
q.pop();
for (int nxt : graph[cur]) {
if (dist[nxt] == INF) { // 아직 방문하지 않은 경우
dist[nxt] = dist[cur] + 1;
q.push(nxt);
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) {
int N, M;
cin >> N >> M;
vector<vector<int>> adj(N + 1), rev(N + 1);
for (int i = 0; i < M; i++) {
int u, v;
cin >> u >> v;
adj[u].push_back(v);
rev[v].push_back(u);
}
// 1번 도시에서 각 도시까지의 최단 거리 계산
vector<int> dist1(N + 1, INF);
bfs(1, adj, dist1);
// N번 도시에서 각 도시까지(역방향 그래프)를 통한 최단 거리 계산
vector<int> dist2(N + 1, INF);
bfs(N, rev, dist2);
// 전체 최단 거리는 1번에서 N번까지의 거리
int shortest = dist1[N];
vector<int> answer;
// 조건: 1번에서 i까지의 거리와 i에서 N까지의 거리 합이 전체 최단 거리에 해당하면 i는 최단 경로상에 있음
for (int i = 1; i <= N; i++) {
if (dist1[i] + dist2[i] == shortest) {
answer.push_back(i);
}
}
sort(answer.begin(), answer.end());
for (size_t i = 0; i < answer.size(); i++) {
cout << answer[i];
if (i != answer.size() - 1)
cout << " ";
}
cout << "\n";
}
return 0;
}반응형