딥러닝: Perception and Multi-Layer Perception(2)
복습:
우선 이전에 내용을 복습하자면

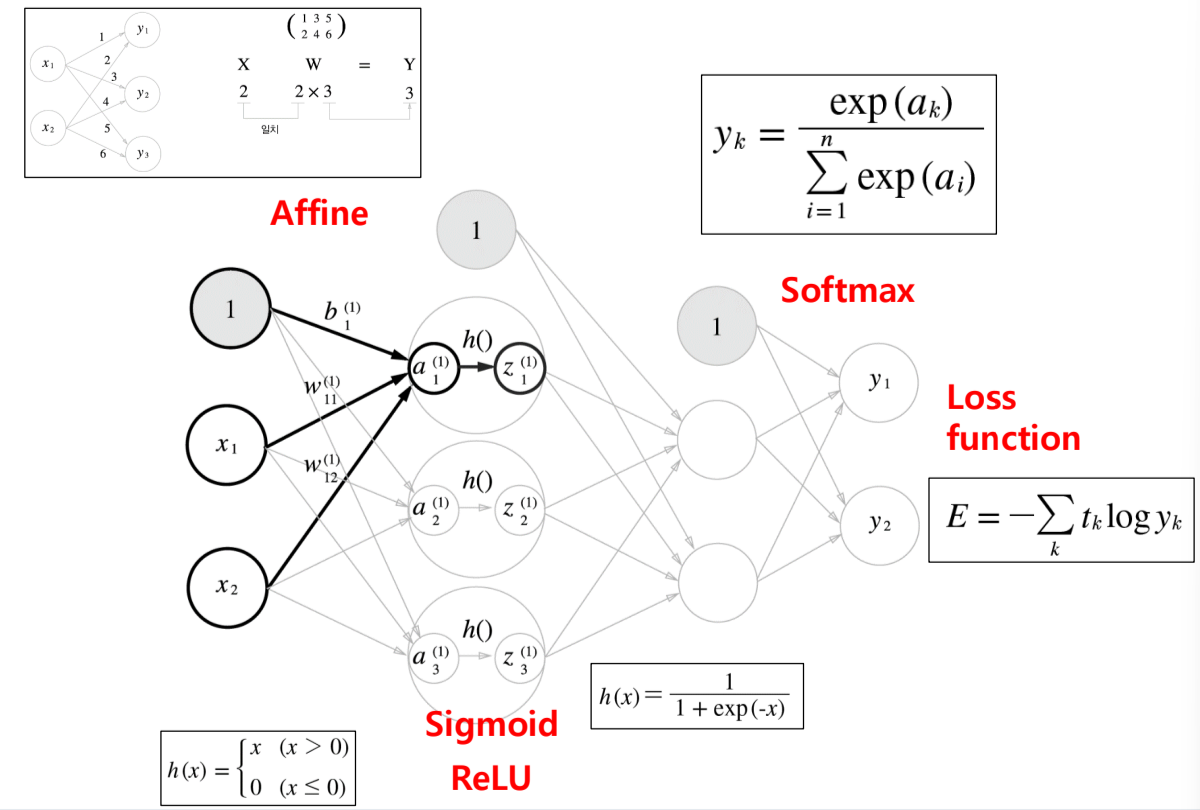
1. Feedforward 를 위해서 각 입력에서 입력받은것을 가중치에 합산해서 sigmoid 나 Relu 로 활성화 함수를 거쳐
마지막 층에서 softmax를 구한후 loss function 으로 Loss를 구해준다.
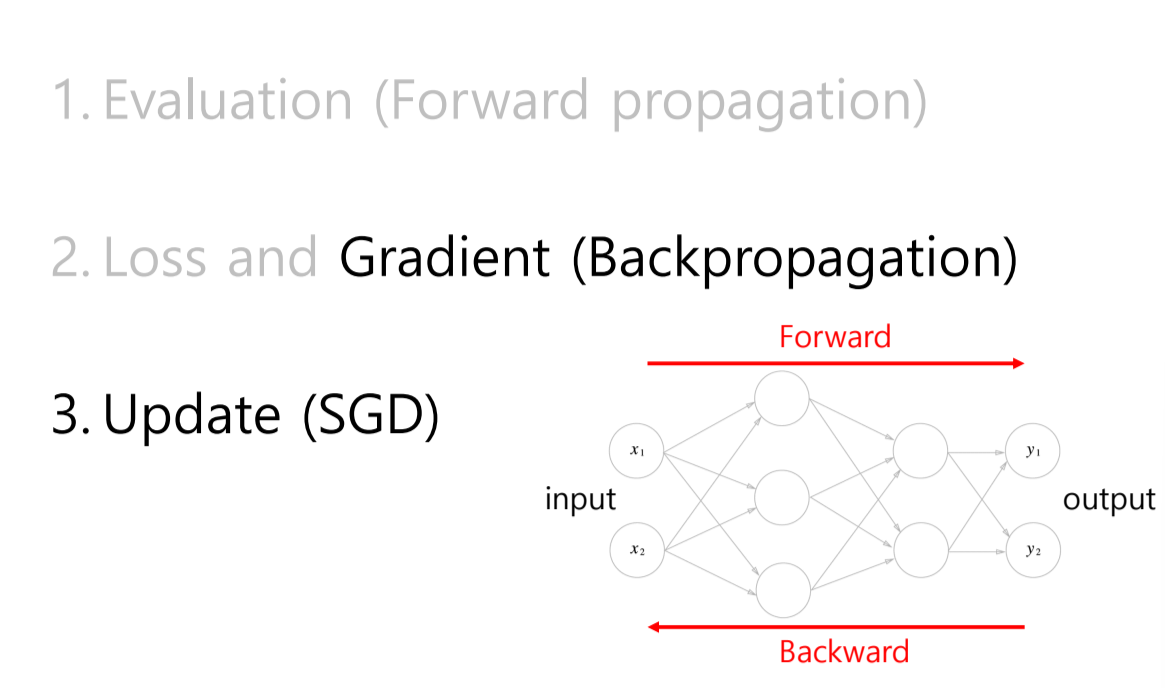
이후에 Backpropagation 을 통해서 가중치들을 업데이트 해준다.
Gradient decent (경사하강법)
자 우리는 이전에 loss (정답과의 오차값) 을 구했다.
그렇다면 우리가 해야 할 것은 이 loss 가 줄어드는 방향으로 가중치를 갱신해줘야 된다는 것이다.
여기서 한가지 드는 의문이 있는데, 가중치의 줄어드는 방향을 어떻게 아는 것인가?
이것은 이제 우리가 미분을 활용하면 된다, 미분은 즉 변화량을 뜻하고
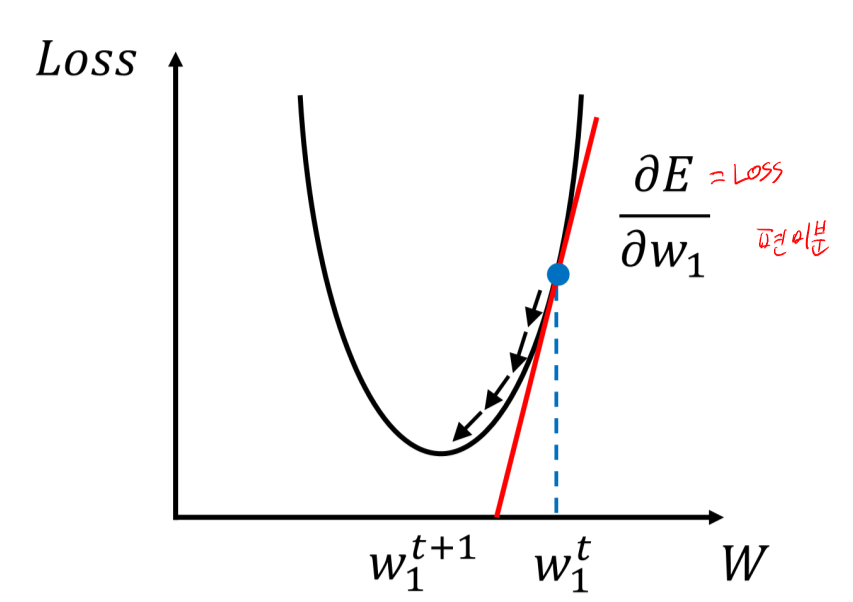
즉 우리는 E에대해서 w 를 편미분해 w가 바뀌었을때 E(loss)가 얼마나 바뀌는지 변화율을 측정할 수 있는 것이다!
그렇다면 우리는 loss를 줄어드는 쪽으로 갱신하다 더이상 갱신이 안되면 최소 오차에 도착한 것일까?
여기서 local minima 란 개념이 등장한다.
Local Minima
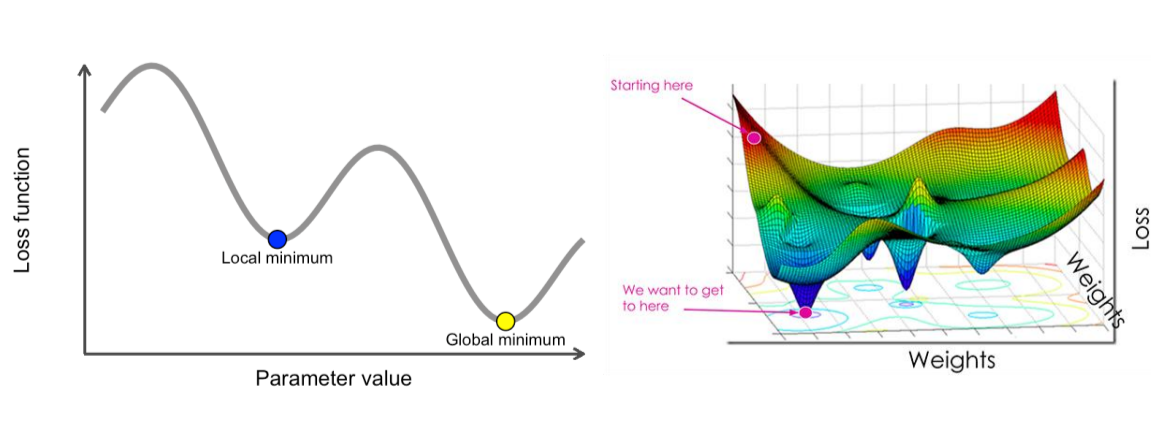
좌측에 보이는 그래프처럼 2차함수가 아닌이상 변곡점이 여러개 나타 날 수 있다.
그렇다면 0이되는 지점이 어려개 나타난다는 것이고
우리가 찾은 0이 되는 지점보다 더 loss가 낮은 지점이 있을 수 있다는 것이다.
가중치가 여러개일때는 우측그림과 같이 매우 복잡해지기 때문에 이를 우리가 직관으로 로컬 미니마를 찾아내는 것은
힘들거라는 것을 짐작 가능하다.
때문에 우리는 경사 하강법을 사용한다.

방법은 바로 기존 가중치에 변화량을

때문에 우리는 Chain Rule을 사용할 것이다.
더하기 Chain Rule
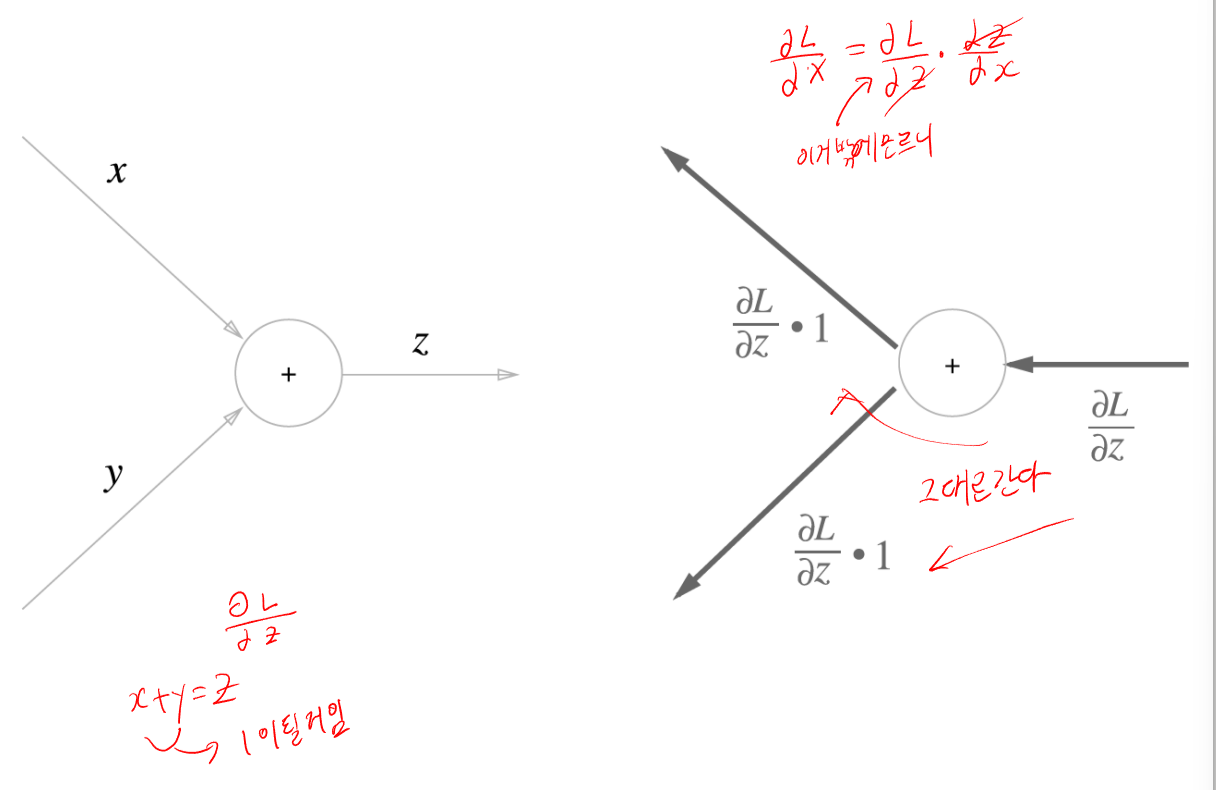

자 우리는 z에대해서 편미분 값을 알고 있는데

이 방법으로 각각 변수에대해서 편미 분 값을 알 수 있다.
근데 여기서 x 와 y가 각각 x에대해서 편미분하면 1
y에 대해서 편미분하면 1이기 때문에 기울기도 그냥 1곱해서 전달하면된다.
곱하기 Chain Rule

곱하기도 같은 방식이다 하지만
xy = z를 편미분하면
각각 y랑 x가 남기 때문에 이걸 곱해서 기울기가 전달된다.
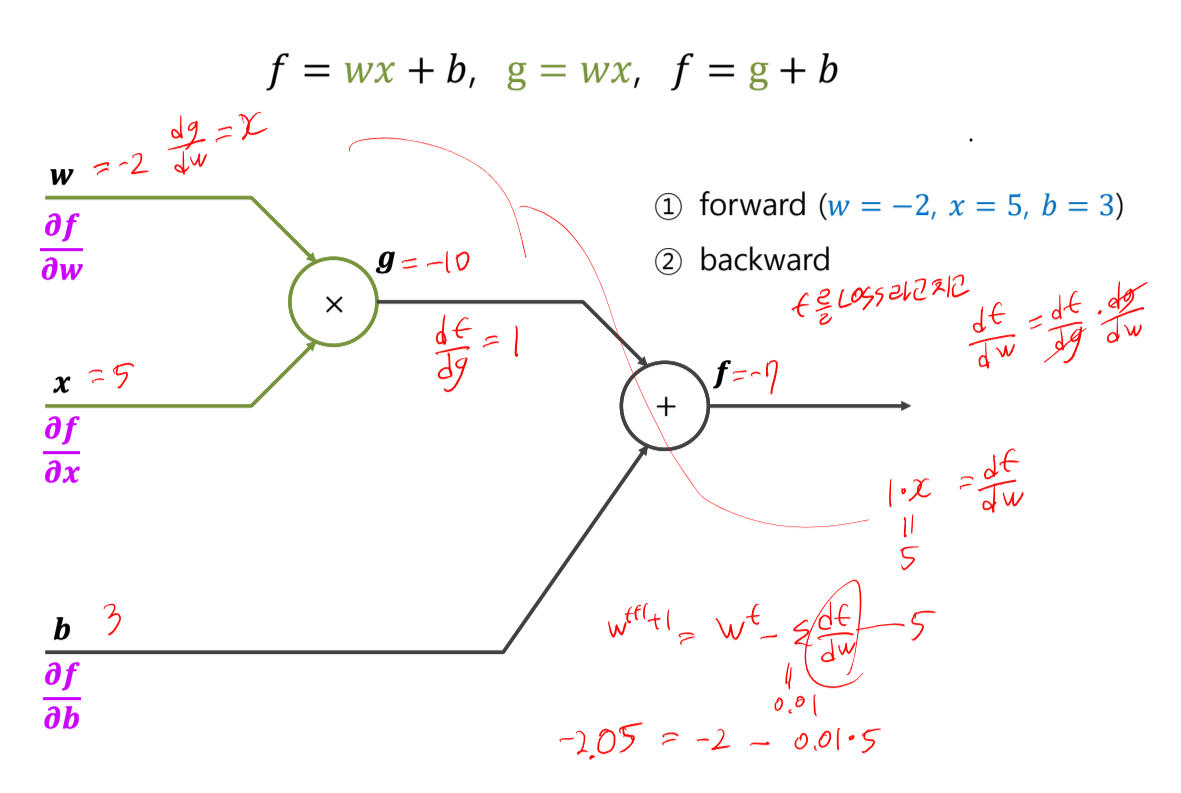
예제도 한번 풀어보자.
시그노이드 미분
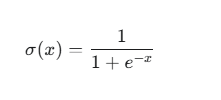
활성화 함수인 시그노이드 함수는 이렇게 생겼다.
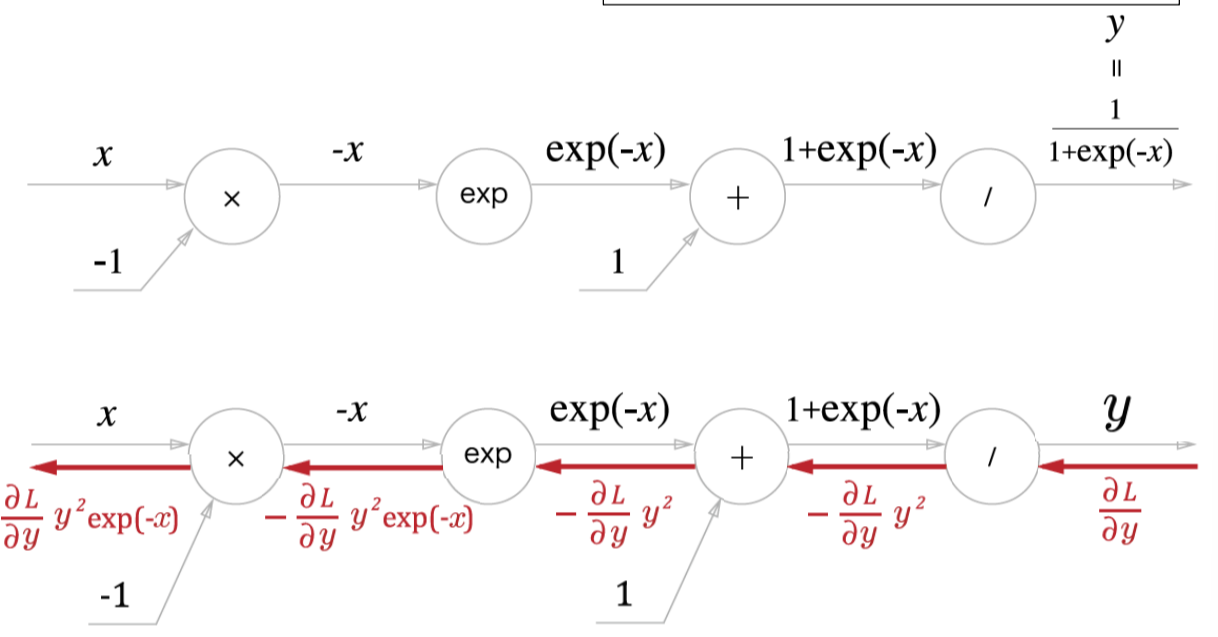
즉 아까와 같은 방식으로 각각 수식을 편미분과정을 거치면
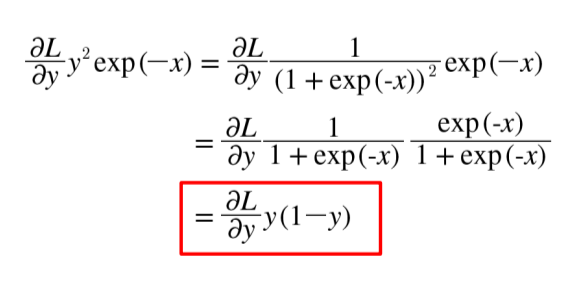
이런 결과물이 나오는걸 알 수 있다.
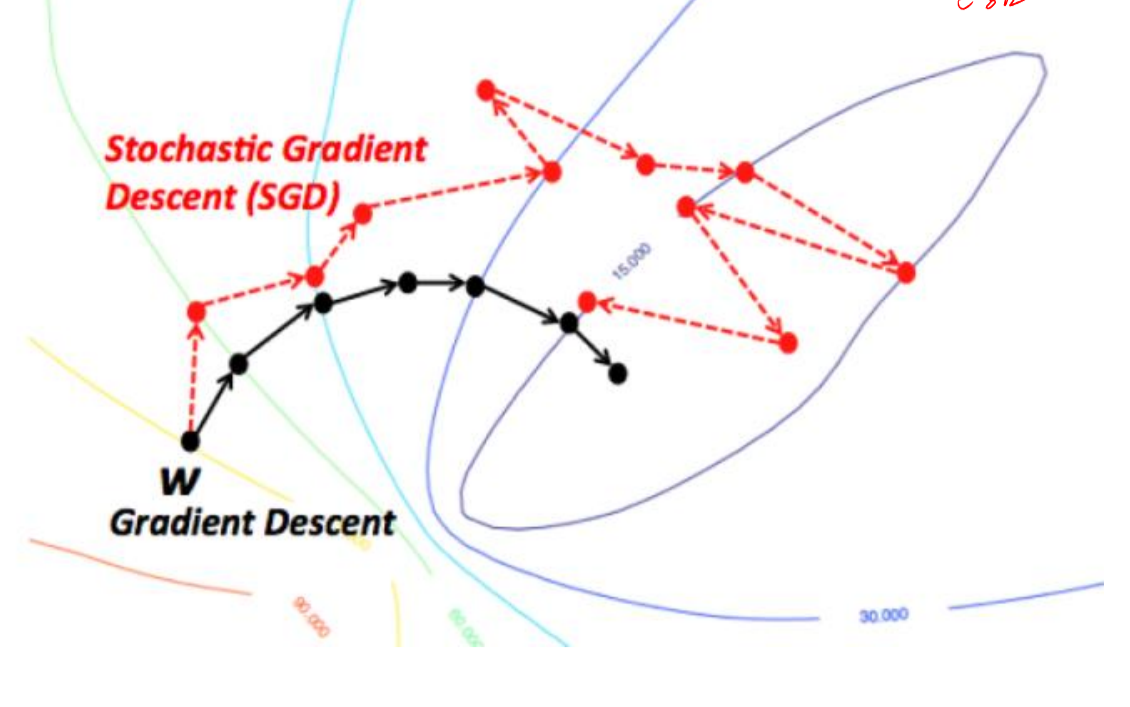
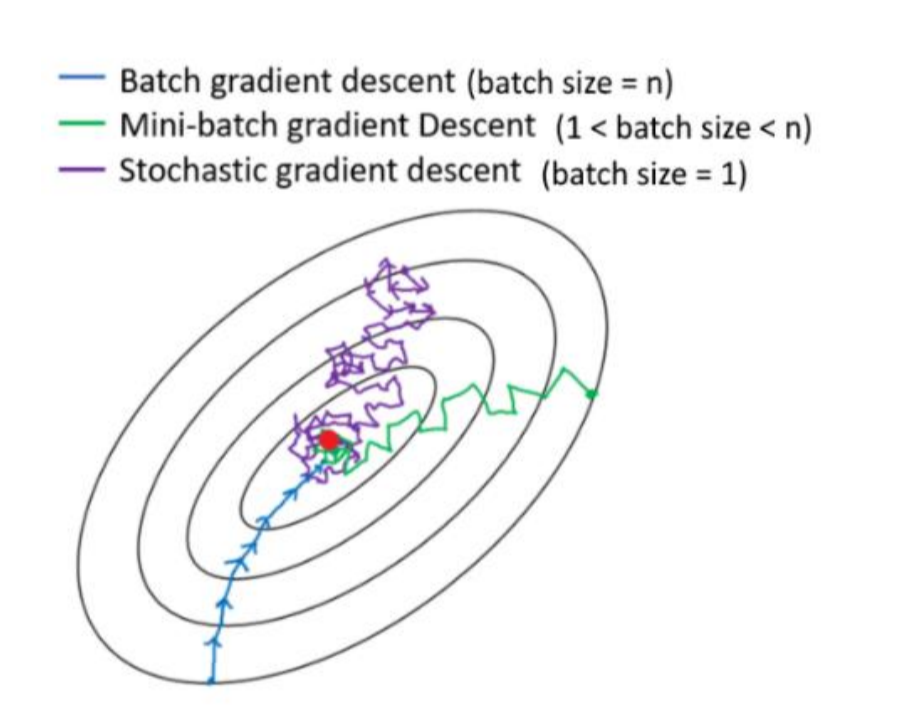
SGD (Stochastic Gradient Descent )
SGD는 확률적으로 여러개중에 하나를 뽑아서 사용하는 것이다
기존의 배치경사하강법은 모든 훈련데이터의 loss의 평균을 사용하지만
이건 샘플중에 하나를 골라서 loss를 계산해 갱신하고
다음 데이터 샘플을 뽑다 반복하는것이지만
매우 불안정하다는 단점이 있다.
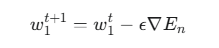
그래서 여기서 배치 단위 = 전체 데이터 사용
미니매치 = 일부 데이터 사용
SGD = 1개사용
으로 볼 수 있고 현대에서는 미니배치 가 가장 많이 사용된다.
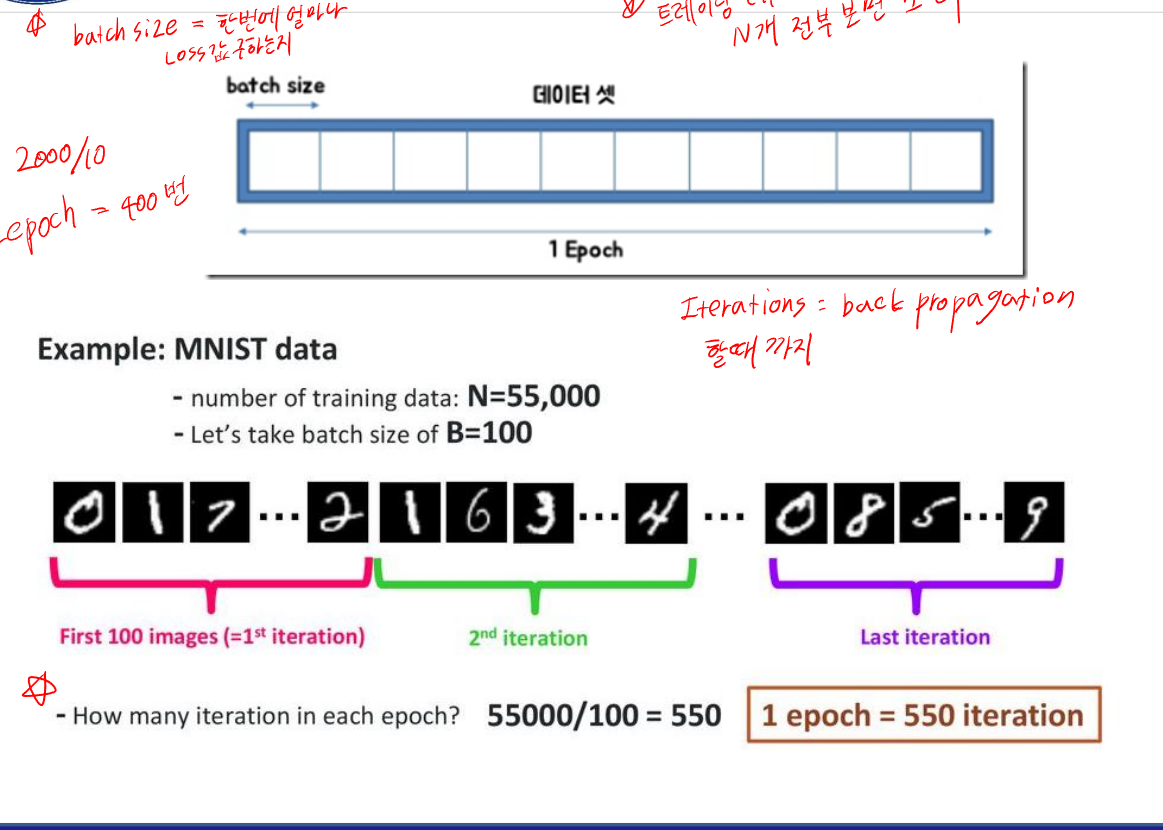
그리고 마지막으로 에포크 , 배치 사이즈 , 이터레이션에 대한 개념을 설명하자면
Epoch : 전체 트레이닝 데이터셋을 처음부터 끝까지 한 번 모두 사용하는 것을 1 Epoch
Batch size : 얼마나 한번에 Loss 값을 구하는지
Iterations : 가중치를 한 번 업데이트하는 과정 ,back propagation 할 때 1 Iteration
로 보면 된다.