딥러닝 : Perception and Multi-Layer Perception (1)
0. 왜 딥러닝을 사용하는가
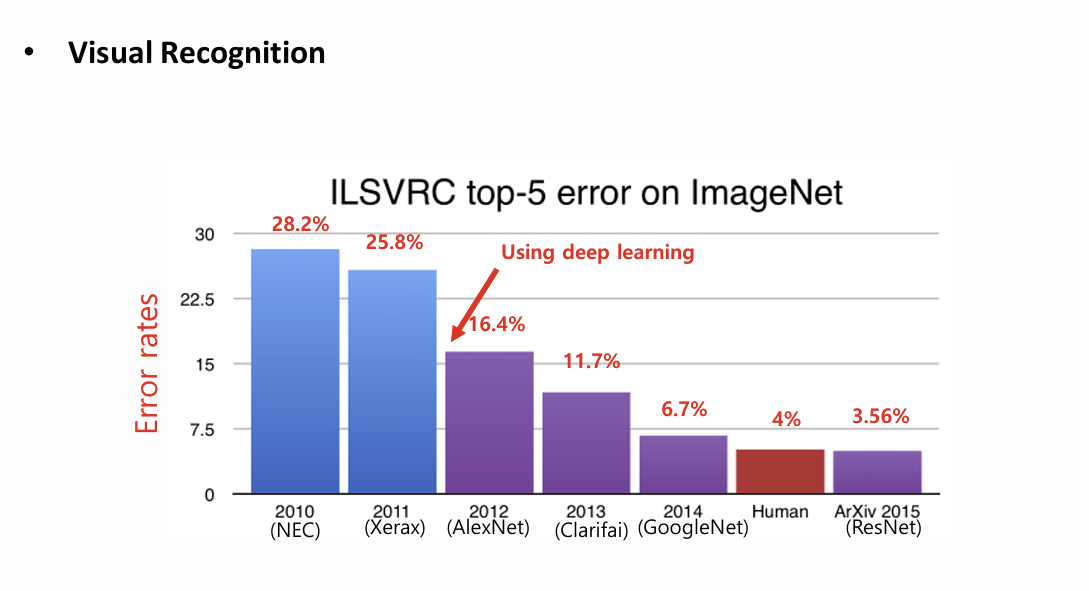
Visual Recognition 오류율 추이이다
2011(Xerax)부터 딥러닝을 사용하기 시작하였는데 이때부터
오류율이 3.56% 까지 급락하였다.
이건 딥러닝을 사용하면서부터 성능이 급격하게 좋아짐을 알 수 있다.
1.어떻게 학습시키나 (How to learn)
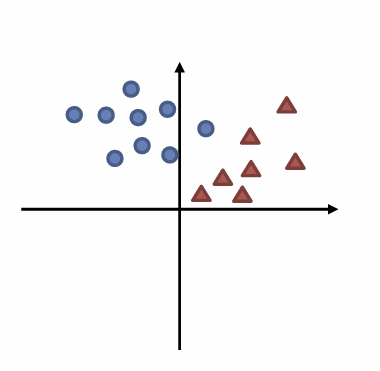
우선 분류 문제를 해결한다고 생각해보자 우리는
동그라미와 삼각형을 분류시키는 선을 그리도록 학습시킬 것이다.
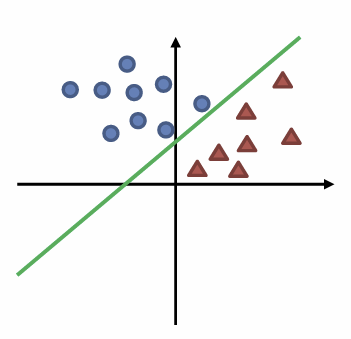
만약 우리가 동그라이미와 삼각형사이에 긋는다면 정답 이다.
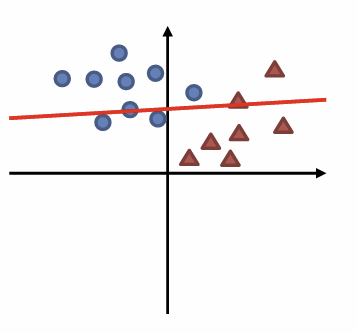
이런식으로 분류하지 못하고 경계를 제대로 찾지 못한다면 오답인 것이다.

자 이번그림도 잘못 그렸지만 이전 그림보다는 더 잘 분류했다고 볼 수 있다.
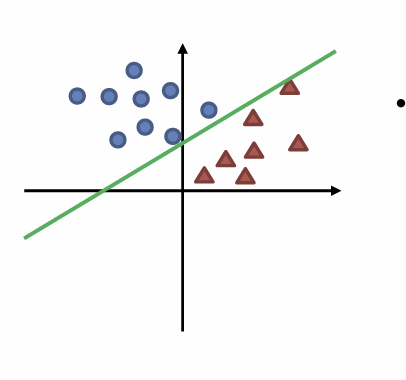
자 이번엔 이전보다 더 학습이 되어서 제대로 라인을 그렸다.
자 이런식으로 단계를 나누자면 3단계로 나눌 수 있을 것이다
1. Make a line 우선 선을 긋는다
2. Find the wrong part 잘못된 부분을 찾는다
3. Modify it 수정한다
자 이 과정을 딥러닝에서는
1.Evaluation(Forward propagation)
2. Loss and Gradient (Backpropagation)
3.Update (SGD)
이 세과정으로 이뤄진다고 생각하면 된다.
첫번째 Evaluation (Forward propagation) 부터 살펴볼건데
그전에 딥러닝의 노드인 Perceptron 부터 알아보도록 하자
Perceptron
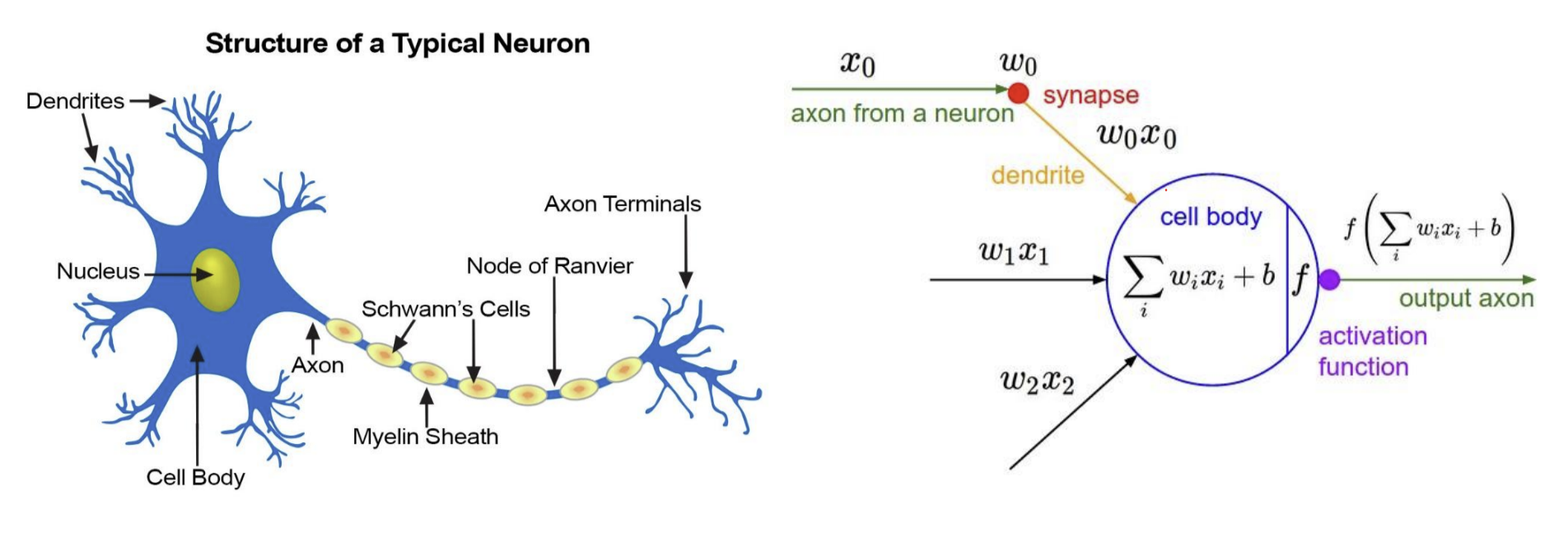
퍼셉트론은 뉴런의 작동방식에서 영감을 받아 만들어져 비슷한 부분이 많다
생물학적 뉴런:
- 수상돌기(dendrite)로 여러 신호를 받음
- 세포체에서 신호들을 합산
- 임계값을 넘으면 축삭(axon)을 통해 신호 전달
- 시냅스를 통해 다른 뉴런에 신호 전달
퍼셉트론:
- 여러 입력값(x₁, x₂, ..., xₙ)을 받음
- 각 입력에 가중치(w₁, w₂, ..., wₙ)를 곱해서 합산
- 편향(bias)을 더한 후 활성화 함수를 통과
- 임계값에 따라 0 또는 1 출력
실제 뉴런은 엄청 복잡하다, 실제로 딥러닝은 뉴런처럼 동작하는게 아니라
매우 단순한 계산 유닛을 수백만 ~수십억개 쌓아서 복잡성을 창발시키기
라고 보면 된다.

위와 같이 input들이 들어오면 각각의 weights를 곱해서 sum 을 구한다.
-> 이때 곱할때 행렬 곱을 사용하면 한번에 구할 수 있기 때문에 행렬 연산을 한다.
이 다음에 이 합에 따라서 0이될지 1이될지 (비활성화 할지 활성화 할지) 를 결정하게 되는데
그건 Activation funtion 으로 결정된다
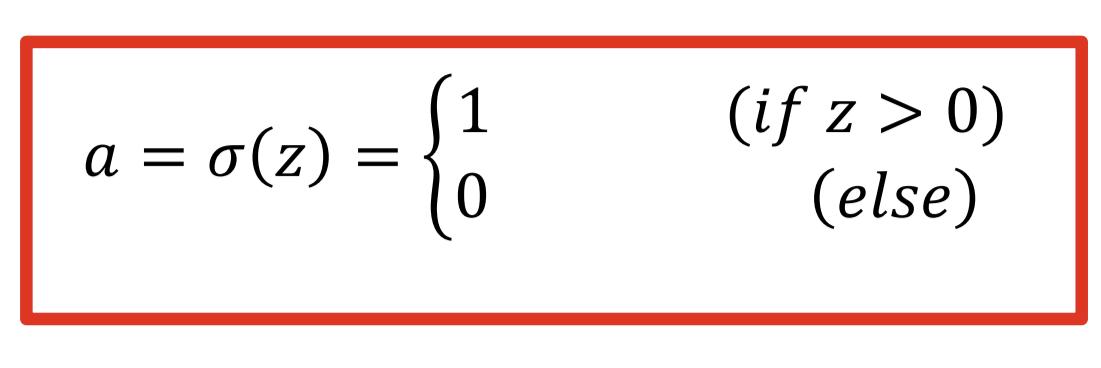
단층 퍼셉트론의 한계

우리 가 만약에
세모와 동그라미를 직선으로 분류하는 문제를 풀게 된다면
단일 퍼셉트론은 직선의 방정식과 똑같기 때문에
이 상태에서 문제를 풀 수 있다.
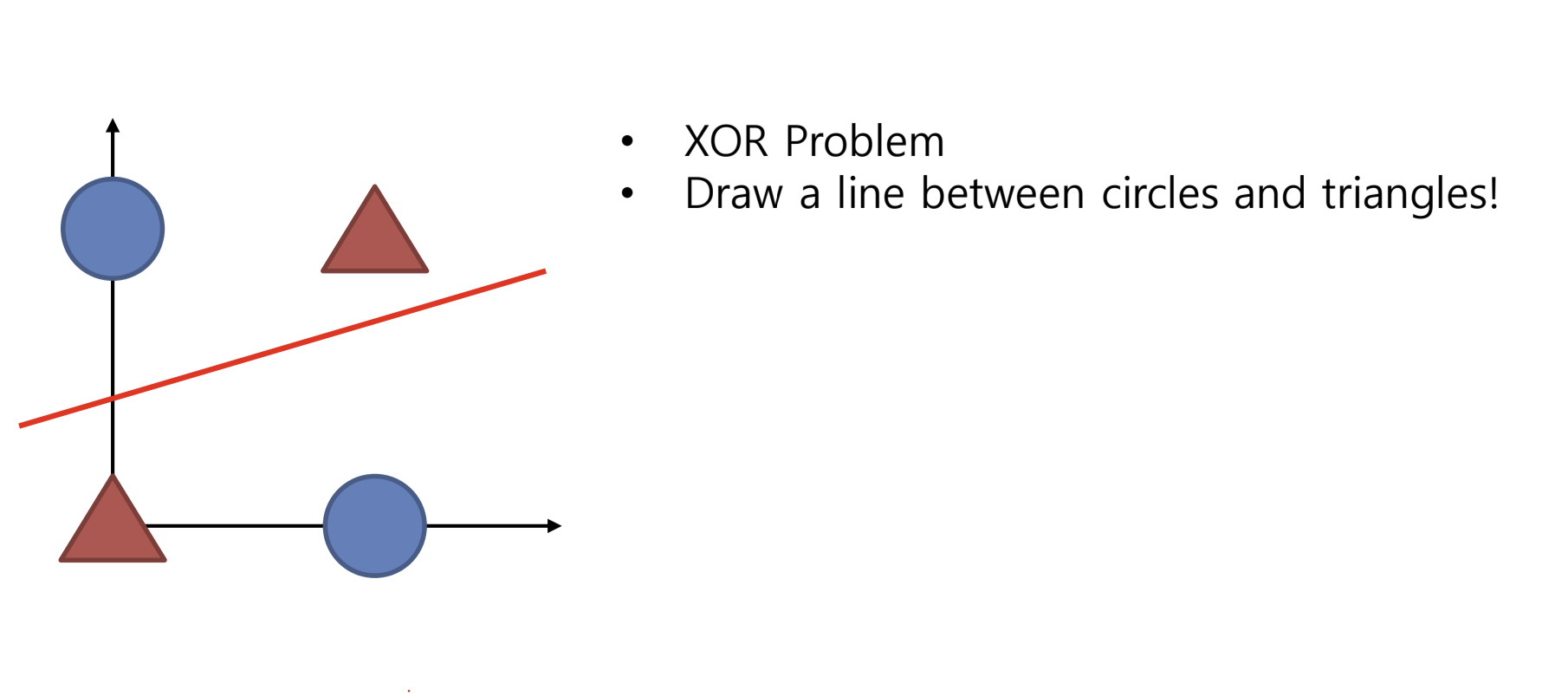
하지만 이렇게 동그라미와 세모가 주어진다면
직선 하나로는 분류 할 수 없게된다.

때문에 직선을 두개 긋는다면 우리는 이 문제를 해결할 수 있을 것이다.
그렇기 때문에 퍼셉트론을 여러개 쌓게 되는것이다.

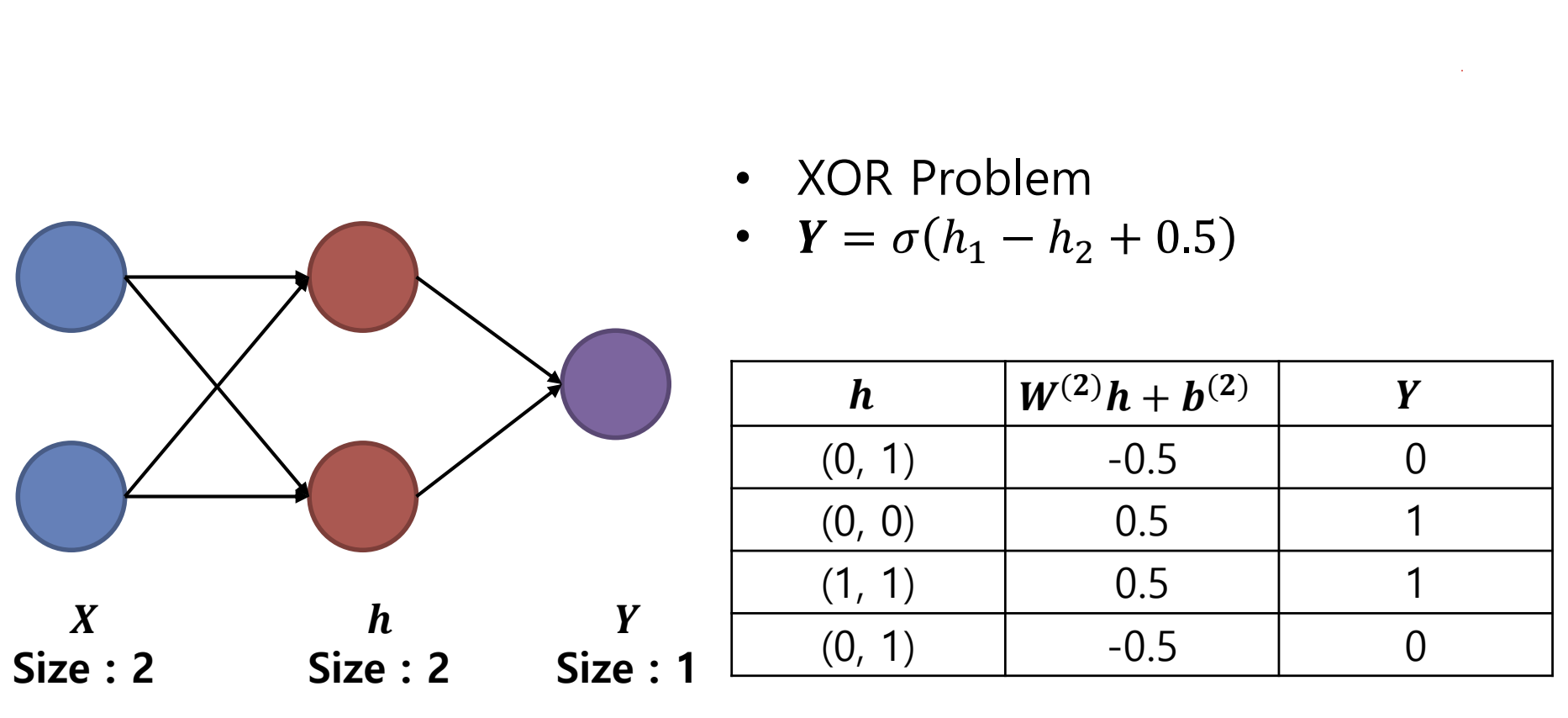
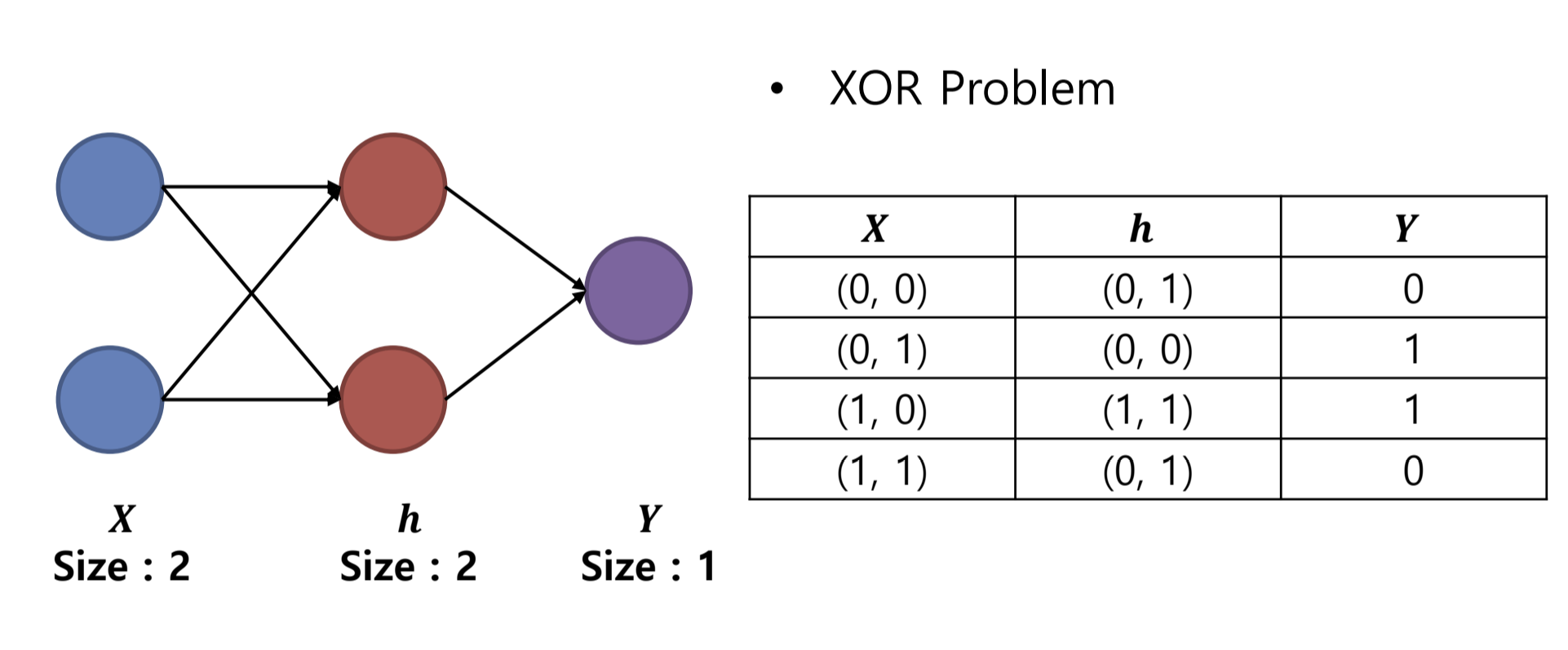
위 그림처럼 우리가 퍼셉트론을 두개 사용한다면
이 xor 문제를 풀 수 있음을 알수 있다.
자 여기서 한가지 의문이 있을 수 있는데
왜 퍼셉트론을 두개 사용하면 가능한지이다.
우선 활성화 함수가 없이 그냥 퍼셉트론을 두개 쓰개되면
그냥 하나의 직선의 방정식과다를게 없는데
활성화 함수 없이 2층을 쌓으면
층1: y = W₁x + b₁
층2: z = W₂y + b₂
이걸 합치면:

그냥 직선의 방정식이라 1개의 퍼셉트론 쓰는것과 다를 것 없게 된다.
이렇게 된다.
다만 활성화 함수를 쓰게되면 어떻게 되는가.
특정값에서 0이되거나 1이된다.
즉 뒤에서 전달되는 값이 갑자기 0이되버리거나 1이 되버려서 뚝 끊기게 되는 것이다
즉 특정값에서 직선이 툭 끊기거나 꺽이게 되는 효과가 난다. (이 끊김이 전달되면서 이후 함수도 학습된다)
때문에 이 꺾인 직선들의 조합이 비선형선을 가지게됨과 동시에 여러 모양을 가질 수 있게 된다 .
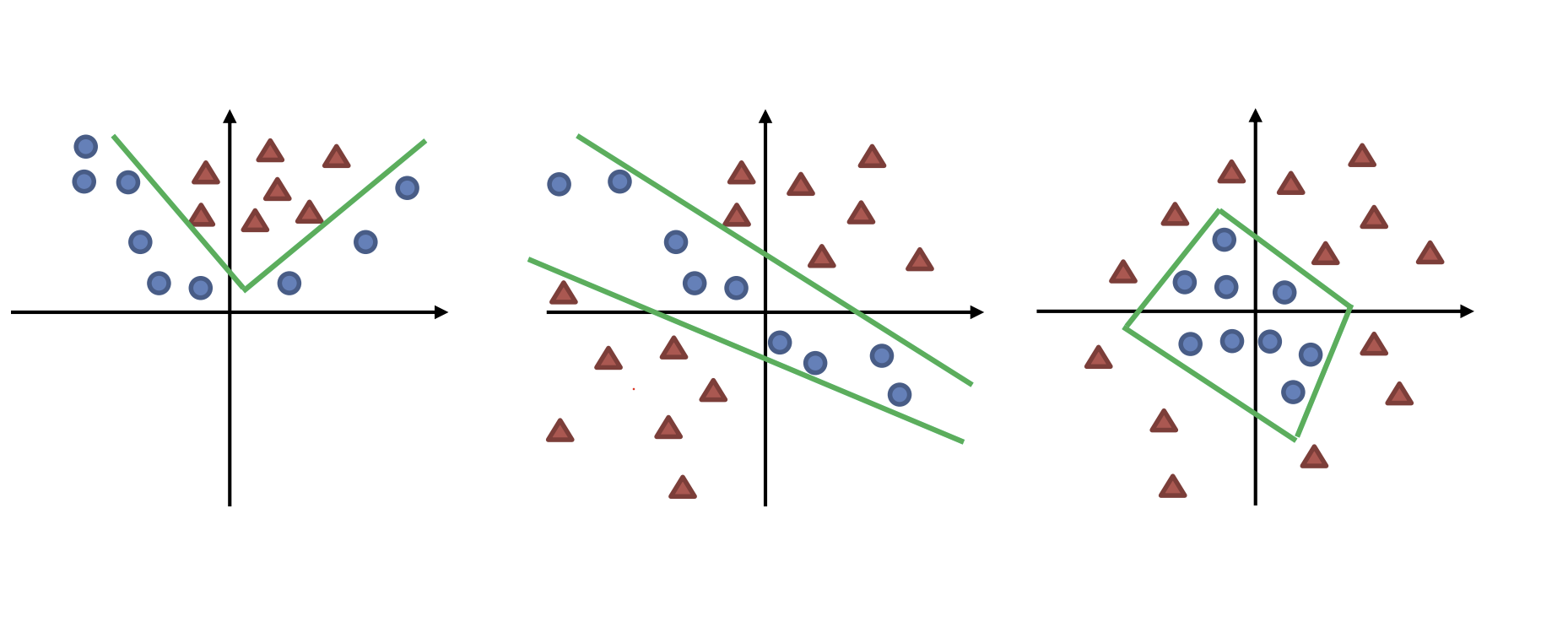
때문에 이런 여러가지 모양을 2개의 퍼셉트론으로 만들 수 있게 된다.
그리고 활성화 함수에는

여러가지 함수가 이렇게 있다.
Softmax
만약 우리가 고양이사진이 주어지고
이것이 고양이인지 아닌지 분류하는 문제를 푼다고 생각하자
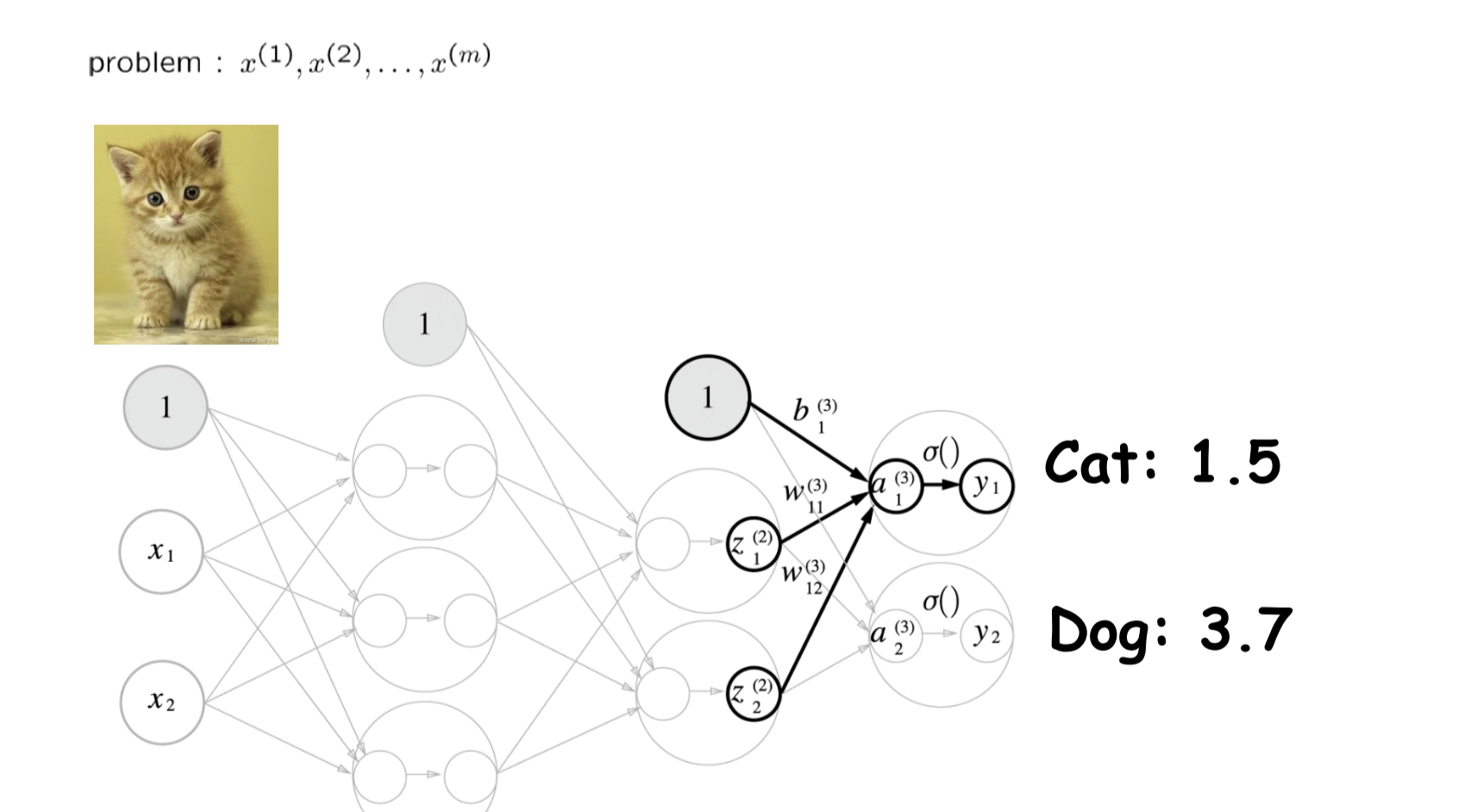
그렇다면 우리는 마지막 층을 2개를 만들어서
개인지 고양이인지 최종 점수를 합산하도록 할 것이다.
그런데 이런 분류 문제에서는 결국 정답을 하나로 축약해야 되기때문에
하나가 얼마나 정답에 가까운지 도출하기위해
확률값으로 바꾼다
이 역할을 하는것이 소프트맥스 함수이다.

Loss function
이번에는 그러면 도출한 정답이 얼마나 오답인지 Loss를 구해서 함수를 갱신해야 되기 때문에
Loss 를 구하는법을 알아보자.
Mean squared error

우리가 출력한 정답에 정답을 빼주고 ( 이경우에는 고양이인것과 아닌것 1과 0 밖에 없다 )
제곱을 해준다 ( 우리는 얼마나 정답과 거리가 있느냐만 중요하기때문에 음수가 나오지 않게 제곱을해준다)
이걸 모든 출력에 적용하고 전부 더해서
정답의 개수만큼 나눠주면 mean square loss를 구할 수 있다.
cross entropy error

크로스 엔트로피 는 예측 확률 분포가 얼마나 실제 확률 분포와 다른가를 측정한다 .

yi 실제 정답인지 여부
^y 정답이라고 예측한 확률
즉 정답이 아니면 로스가 0이되어 갱신되지않고
실제 정답이라고 낮게 생각할수록 값이 커지기 된다.
즉 정답을 얼마나 덜 정답이라고 유추하냐에 따라서 값이 커진다고 보면 된다.