반응형
https://www.acmicpc.net/problem/9764
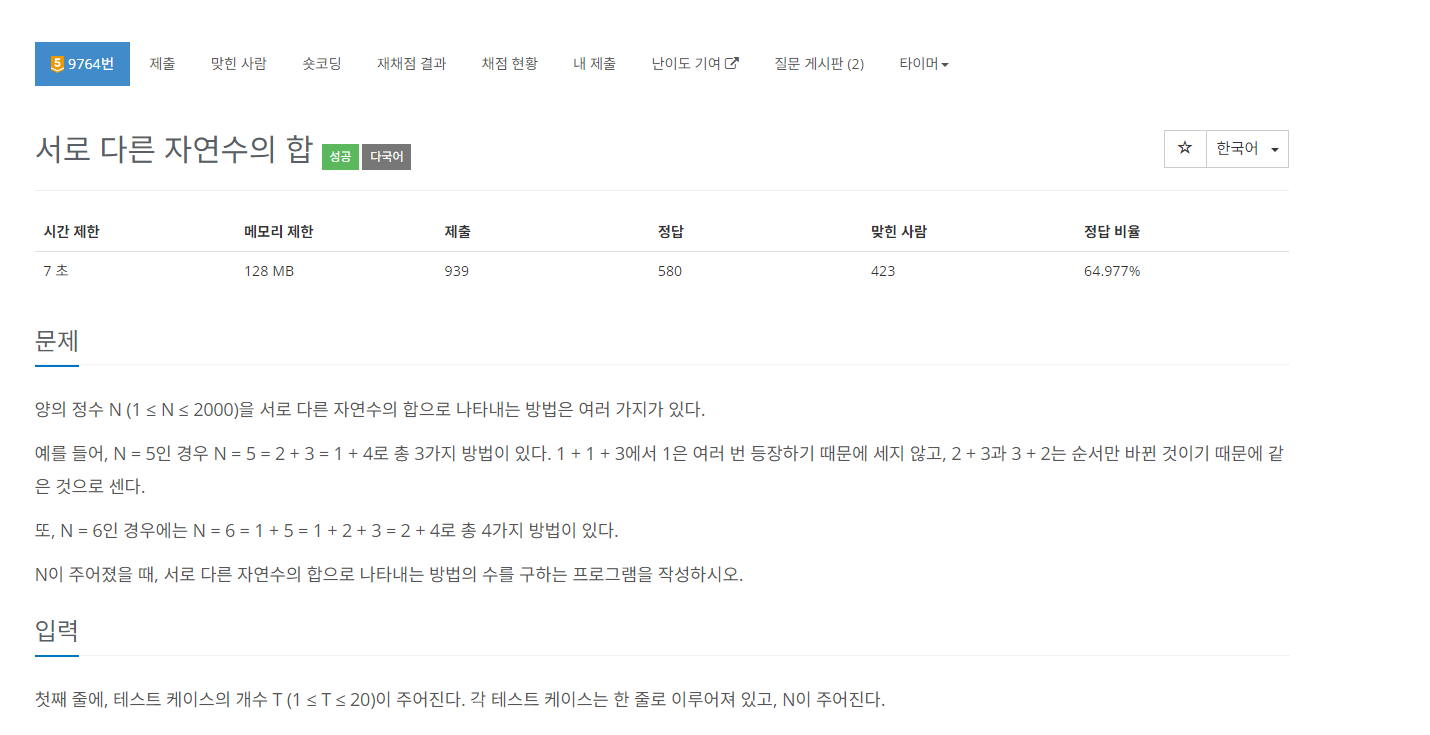
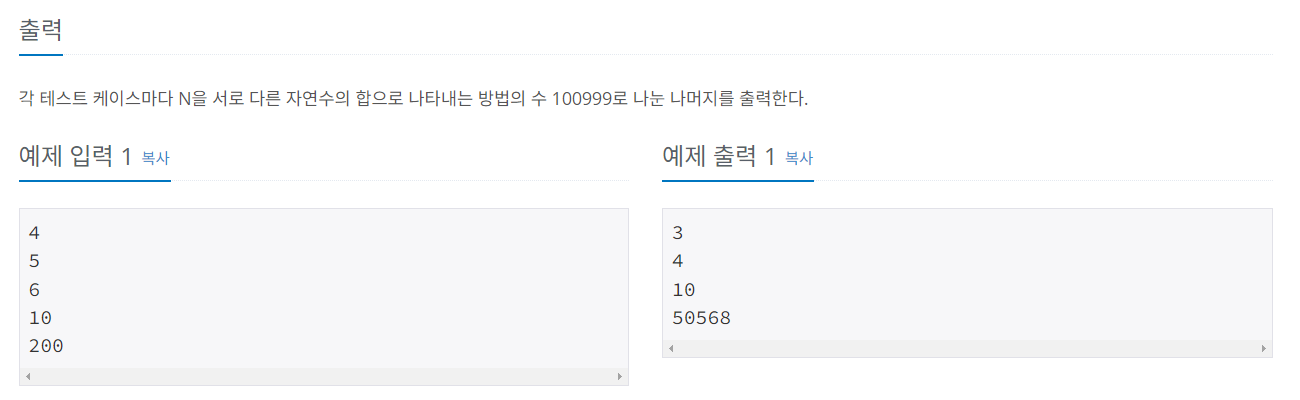
#문제 간단 정리
#문제 해결 방법
우선 동적 계획법을 사용해야된다는건 쉽게 알아차릴 수 있다
왜냐면
1. 중복되는 부분 문제(Overlapping Subproblems)
2. 최적 부분 구조(Optimal Substructure)
를 n의 조합을 알기 위해서는 이전의 수가 필요하고 이전의 수 조합으로 구할 수 있다는 것을 쉽게 알 수 있기 때문이다.
그렇다면 선택할수 있는건
그 수의 조합을 만들기 위해 어떤수를 사용하던가 사용하지 않던가
로 나뉜다는 것을 알 수 있다.
// dp[i][j] 1~j의 수들의 합으로 i 를 만드는 방법의수
// 1. j를 포함하지 않고 만드는경우
// dp[i][j-1];
// 2. j를 포함해서 i를 만드는경우
// if(i>=j) D[i][j] = (D[i][j] + D[i-j][j-1]) % mod ;
// D[i-j][j-1] = i-j를 1 ~ j-1 사이의 수들로 만드는방법의 수
#전체 코드
#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;
#define MOD 100999
int dp[2001][2001];
int main() {
int t;
int n;
// dp[i][j] 1~j의 수들의 합으로 i 를 만드는 방법의수
// 1. j를 포함하지 않고 만드는경우
// dp[i][j-1];
// 2. j를 포함해서 i를 만드는경우
// if(i>=j) D[i][j] = (D[i][j] + D[i-j][j-1]) % mod ;
// D[i-j][j-1] = i-j를 1 ~ j-1 사이의 수들로 만드는방법의 수
dp[0][0] = 1;
for (int i = 1; i < 2001; i++) {
dp[i][0] = 0;
dp[0][i] = 1;
}
for (int i = 1; i < 2001; i++) {
for (int j = 1; j < 2001; j++) {
dp[i][j] = dp[i][j - 1]; //j를 포함하지 않고 i를 만드는 경우
if (i >= j) {
dp[i][j] += dp[i - j][j - 1];
dp[i][j] %= MOD;
}
}
}
cin >> t;
while (t--) {
cin >> n;
cout << dp[n][n] << endl;
}
return 0;
}반응형
'[백준] > C++' 카테고리의 다른 글
| 백준 9764번 서로 다른 자연수의 합 [C++] (0) | 2024.09.13 |
|---|---|
| 백준 4358번 생태학 [C++] (0) | 2024.09.13 |
| 백준 10026번 적록색약 [C++] (0) | 2024.09.07 |
| 백준 2589번 보물섬 [C++] (0) | 2024.09.05 |
| 백준 25601번 자바의 형변환 [C++] (0) | 2024.08.30 |
