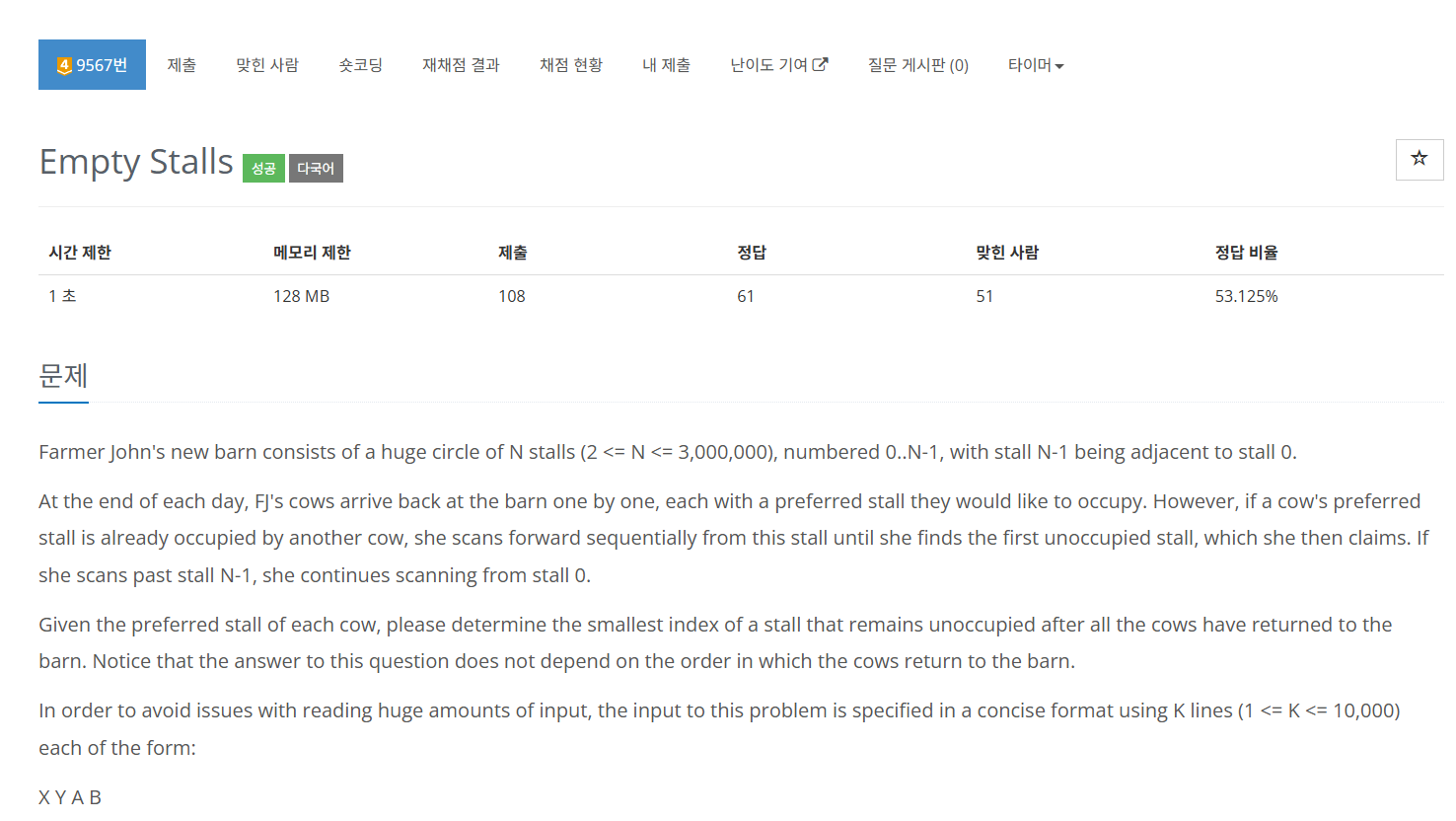
반응형
https://www.acmicpc.net/problem/9567
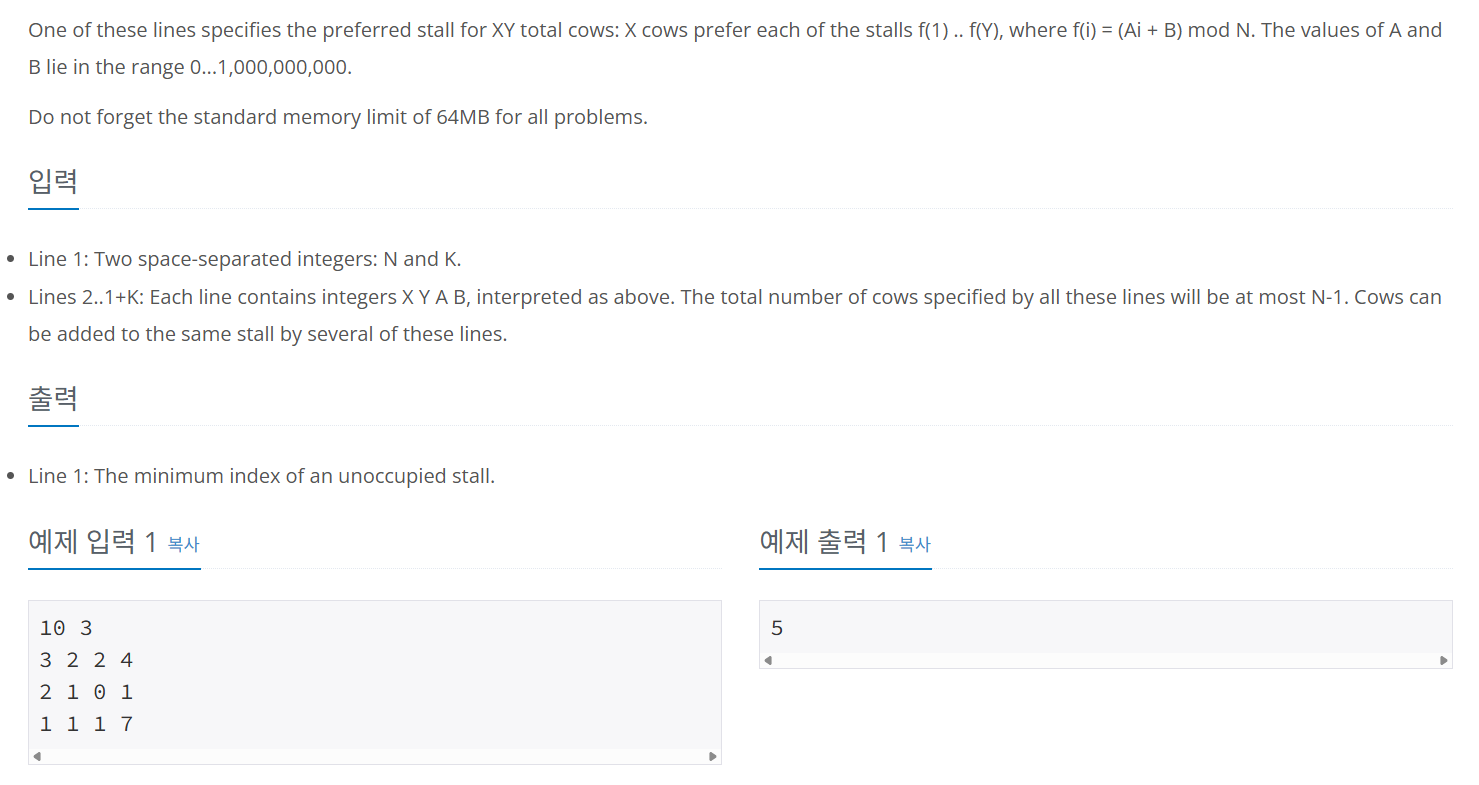

#번역

#문제 간단 정리
#문제 해결 방법
우선 입력이 들어오면 A번째 축사를 선호하는 몇마리가 들어오는지 알게 되는데
이걸 배열에다가 누적해서 기록을 해두자
0 1 2 3 4 5 6 7 8 9 축사가 있으면
3번째좋아하는 소가 3마리
6번째 좋아하는 소가 3마리
6번쨰 좋아하는 소가 3마리 들어오면
0 1 2 3 4 5 6 7 8 9 :축사 번호
0 0 0 3 0 0 6 0 0 0 : 소 누적 배열
이런식으로 누적을 해준 후에
목장을 2번 돌면서
cowStack 이란 변수를 선언해주고 (현재 대기하고 있는 소들 누적 변수)
누적배열에 소가 잇다면 소를 더해주고
(예를들어 i = 3 이고 누적배열[3] 에 소가 0 이상이라면 더해주면 된다)
bool 배열로 비어있는지 체크해서 비어있다면 ( 그 목초지에 소가 들어있는지 확인)
소를 한마리 넣어주고 cowStack-- 를 해주면 ( bool 배열은 true 로 바꿔줌)
모든 소가 제자리를 찾아가게 된다
뭐 대략 벡터 선언에 3백만씩 들고
2번 순회하는데 3백만*2
시간 복잡도는 충분해 보인다.
다만 2번 순회한다는 생각은 상당히 그리디같은 생각이긴한데
딱히 반례가 없기때문에 2번으로 잡았다.
그리고 또 주의해야 할 점은 자료형 크기인데
n = 3백만
A 와 B 가 최대 10억으로 들어오고
XY가 대략 N까지 될수 있을거기 떄문에
10억 * 3백만이라서
long long 타입을 써줘야 되는걸 주의해야된다.
#전체 코드
#include <iostream>
#include <unordered_map>
#include <string>
#include <sstream>
#include <map>
#include <climits>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, k;
cin >> n >> k;
vector<ll> stallWait(n,0);
vector<bool> cowIsIn(n, false);
for (int i = 0; i < k; i++) {
ll x, y, a, b;
cin >> x >> y >> a >> b;
//그 목초지의 대기 소 추가
for (ll j = 1; j <= y; j++) {
ll temp = ((a * j) + b) % n;
stallWait[temp] += x;
//cout << "temp :" << temp << '\n';
}
}
//두번정도 돌면 전부 해소할거같음
ll cowStack = 0;
int minNumStall = INT_MAX;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < n; j++) {
if (stallWait[j] != 0) {
cowStack += stallWait[j];
stallWait[j] = 0;
}
if (cowIsIn[j] == false && cowStack >0) {
cowStack--;
cowIsIn[j] = true;
//cout << j << ' ';
}
}
}
for (int i = 0; i < n; i++) {
if (cowIsIn[i] == false) {
minNumStall = i;
break;
}
}
cout << minNumStall << '\n';
return 0;
}반응형
'[백준] > C++' 카테고리의 다른 글
| 백준 8983번 사냥꾼 [C++] (0) | 2025.03.27 |
|---|---|
| 백준 28333번 화이트 칼라 [C++] (0) | 2025.03.18 |
| 백준 15811번 복면산?! [C++] (0) | 2025.03.13 |
| 백준 12786 INHA SUIT [C++] (0) | 2025.03.06 |
| 백준 14575번 뒤풀이 [C++] (0) | 2025.03.02 |
