반응형
https://www.acmicpc.net/problem/32823
#문제 간단 정리
CCW + 수학 문제
#문제 해결 방법
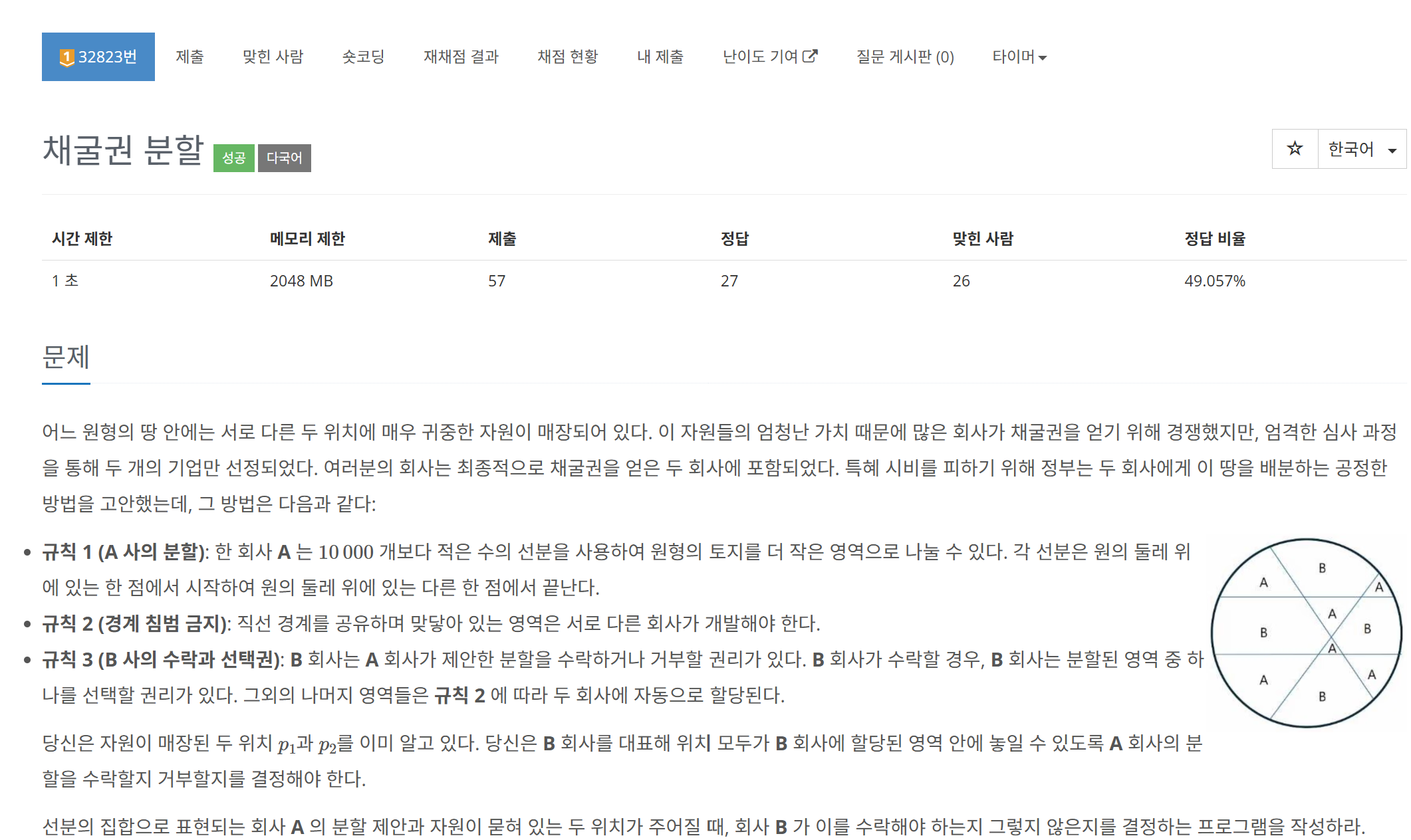
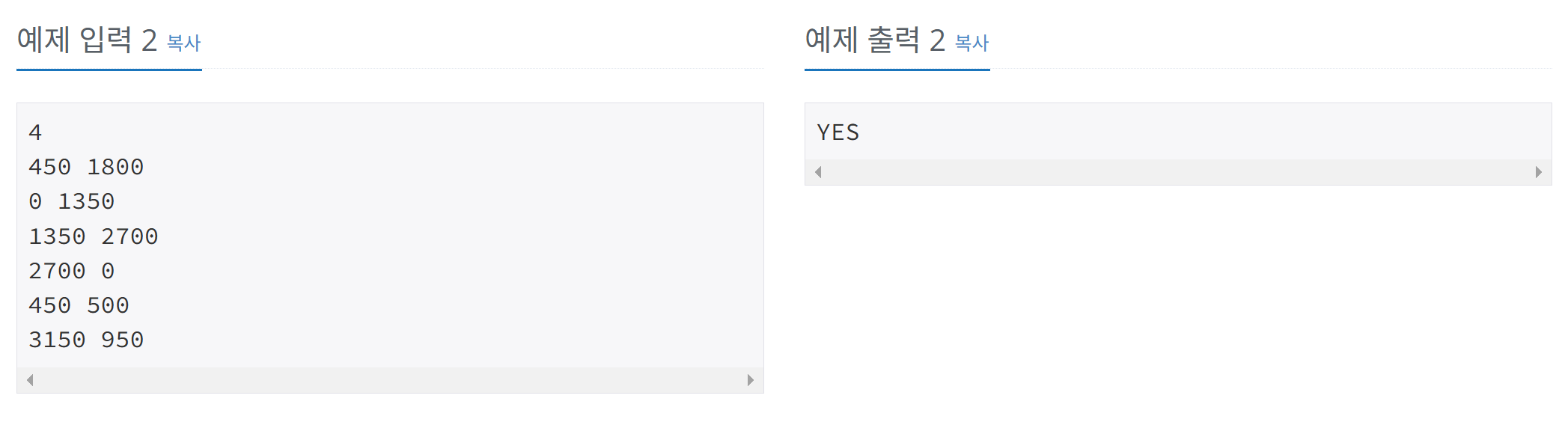
우선 관찰을 하면 p1 p2 두 점 사이에 선분이
홀수개면 둘 다 채굴 불가
짝수개면 둘 다 채굴 가능인 것을 알 수 있다.
때문에 두 점 사이에 선분이 몇개가 있는지 확인하면 되는데
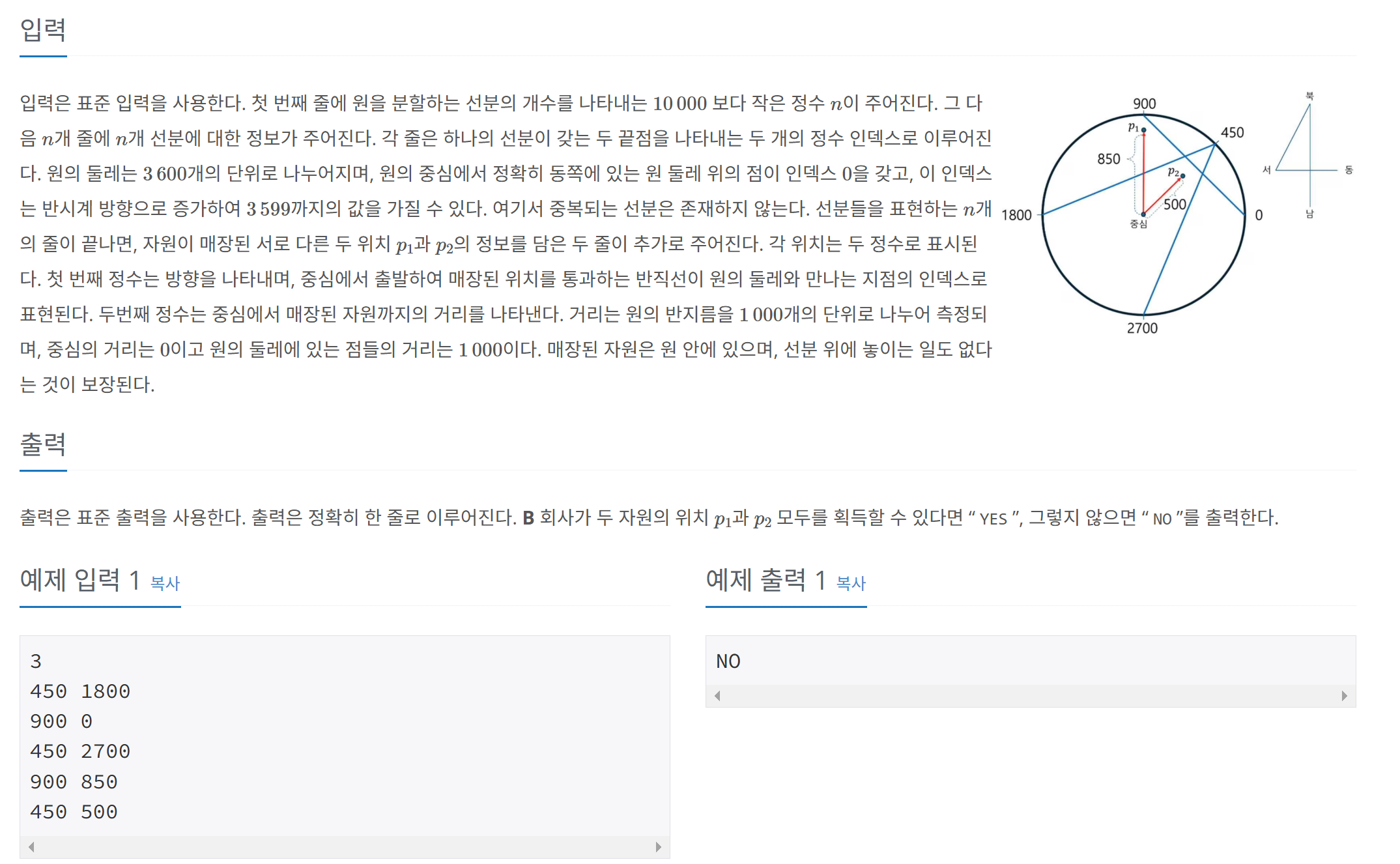
CCW 를 활용하기 위해서 각 좌표들을 삼각함수를 사용해 극좌표를 직교좌표로 변경해준다
그런데 tan로 y좌표를 구하면 무한대가 되버리니
sin 으로 y좌표를 구해주고
각 선분에 대해서 p1 p2 에 대해서 ccw로 교차 판정을 해주면 된다
삼각함수 변경하는 부분에서 실수 오차가 날수 있으니 주의해 줘야된다.
#전체 코드
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long double ld;
#define M_PI 3.14159265358979323846
int ccw(ld x1, ld y1, ld x2, ld y2, ld x3, ld y3) {
ld crossProduct = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1);
if (crossProduct > 0) {
return 1;
} else if (crossProduct < 0) {
return -1;
} else {
return 0;
}
}
// 메인 함수
int main() {
int n;
vector<pair<pair<ld, ld>, pair<ld, ld>>> lines;
cin >> n;
for (int i = 0; i < n; i++) {
ld a, b;
cin >> a >> b;
ld radianA = (a * M_PI) / 1800.0;
ld radianB = (b * M_PI) / 1800.0;
ld transX1 = cos(radianA) * 1000;
ld transY1 = sin(radianA) * 1000;
ld transX2 = cos(radianB) * 1000;
ld transY2 = sin(radianB) * 1000;
lines.push_back({{transX1, transY1}, {transX2, transY2}});
}
int crossCount = 0;
ld p1, p2, p1Length, p2Length;
cin >> p1 >> p1Length >> p2 >> p2Length;
ld radianP1 = (p1 * M_PI) / 1800.0;
ld radianP2 = (p2 * M_PI) / 1800.0;
ld p1X = cos(radianP1) * p1Length;
ld p1Y = sin(radianP1) * p1Length;
ld p2X = cos(radianP2) * p2Length;
ld p2Y = sin(radianP2) * p2Length;
for (int i = 0; i < lines.size(); i++) {
ld x1 = lines[i].first.first, y1 = lines[i].first.second;
ld x2 = lines[i].second.first, y2 = lines[i].second.second;
int thirdCCW = ccw(x1, y1, x2, y2, p1X, p1Y);
int fourthCCW = ccw(x1, y1, x2, y2, p2X, p2Y);
if (thirdCCW == 0 || fourthCCW == 0) {
continue;
}
if (thirdCCW * fourthCCW < 0) {
crossCount++;
}
}
cout << ((crossCount % 2) == 0 ? "YES" : "NO");
return 0;
}반응형
'[백준] > C++' 카테고리의 다른 글
| 백준 15559번 내 선물을 받아줘 [C++] (0) | 2024.12.14 |
|---|---|
| 백준 4347번 Tic Tac Toe [C++] (0) | 2024.12.13 |
| 백준 15752번 Hoofball [C++] (0) | 2024.11.25 |
| 백준 2193번 이친수 [C++] (0) | 2024.10.07 |
| 백준 7861번 Longest Ordered Subsequence [C++] (0) | 2024.10.05 |
반응형
https://www.acmicpc.net/problem/32823



#문제 간단 정리
CCW + 수학 문제
#문제 해결 방법
우선 관찰을 하면 p1 p2 두 점 사이에 선분이
홀수개면 둘 다 채굴 불가
짝수개면 둘 다 채굴 가능인 것을 알 수 있다.
때문에 두 점 사이에 선분이 몇개가 있는지 확인하면 되는데
CCW 를 활용하기 위해서 각 좌표들을 삼각함수를 사용해 극좌표를 직교좌표로 변경해준다
그런데 tan로 y좌표를 구하면 무한대가 되버리니
sin 으로 y좌표를 구해주고
각 선분에 대해서 p1 p2 에 대해서 ccw로 교차 판정을 해주면 된다
삼각함수 변경하는 부분에서 실수 오차가 날수 있으니 주의해 줘야된다.
#전체 코드
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
typedef long double ld;
#define M_PI 3.14159265358979323846
int ccw(ld x1, ld y1, ld x2, ld y2, ld x3, ld y3) {
ld crossProduct = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1);
if (crossProduct > 0) {
return 1;
} else if (crossProduct < 0) {
return -1;
} else {
return 0;
}
}
// 메인 함수
int main() {
int n;
vector<pair<pair<ld, ld>, pair<ld, ld>>> lines;
cin >> n;
for (int i = 0; i < n; i++) {
ld a, b;
cin >> a >> b;
ld radianA = (a * M_PI) / 1800.0;
ld radianB = (b * M_PI) / 1800.0;
ld transX1 = cos(radianA) * 1000;
ld transY1 = sin(radianA) * 1000;
ld transX2 = cos(radianB) * 1000;
ld transY2 = sin(radianB) * 1000;
lines.push_back({{transX1, transY1}, {transX2, transY2}});
}
int crossCount = 0;
ld p1, p2, p1Length, p2Length;
cin >> p1 >> p1Length >> p2 >> p2Length;
ld radianP1 = (p1 * M_PI) / 1800.0;
ld radianP2 = (p2 * M_PI) / 1800.0;
ld p1X = cos(radianP1) * p1Length;
ld p1Y = sin(radianP1) * p1Length;
ld p2X = cos(radianP2) * p2Length;
ld p2Y = sin(radianP2) * p2Length;
for (int i = 0; i < lines.size(); i++) {
ld x1 = lines[i].first.first, y1 = lines[i].first.second;
ld x2 = lines[i].second.first, y2 = lines[i].second.second;
int thirdCCW = ccw(x1, y1, x2, y2, p1X, p1Y);
int fourthCCW = ccw(x1, y1, x2, y2, p2X, p2Y);
if (thirdCCW == 0 || fourthCCW == 0) {
continue;
}
if (thirdCCW * fourthCCW < 0) {
crossCount++;
}
}
cout << ((crossCount % 2) == 0 ? "YES" : "NO");
return 0;
}반응형
'[백준] > C++' 카테고리의 다른 글
| 백준 15559번 내 선물을 받아줘 [C++] (0) | 2024.12.14 |
|---|---|
| 백준 4347번 Tic Tac Toe [C++] (0) | 2024.12.13 |
| 백준 15752번 Hoofball [C++] (0) | 2024.11.25 |
| 백준 2193번 이친수 [C++] (0) | 2024.10.07 |
| 백준 7861번 Longest Ordered Subsequence [C++] (0) | 2024.10.05 |
