https://www.acmicpc.net/problem/15423

#한국어 번역
설명:
화폐 시스템 S는 실제 또는 가상의 화폐 시스템에서 동전의 값을 나타내는 고유한 양의 정수들의 유한 집합(비어있지 않은 집합)입니다. 예를 들어, 캐나다에서 사용되는 화폐 시스템은 {1, 5, 10, 25, 100, 200}으로, 1은 1센트 동전을 나타내고 200은 2달러(200센트)를 나타냅니다. 우리는 동전이 무한히 많다고 가정하며, S에는 항상 1이 포함된다고 가정합니다. 1이 포함된다는 것은 모든 양의 정수를 동전들의 합으로 표현할 수 있음을 보장합니다.
전 세계의 계산원들은 다음과 같은 문제에 직면합니다: 주어진 화폐 시스템과 고객에게 갚아야 할 양의 정수 금액이 있을 때, 정확히 그 금액을 맞추기 위해 필요한 최소 동전의 수는 얼마인가? 예를 들어, 캐나다의 계산원이 고객에게 83센트를 갚아야 한다고 가정합시다. 한 가지 가능한 방법은 25+25+10+10+10+1+1+1, 즉 8개의 동전을 주는 것이지만, 이는 최적의 방법이 아닙니다. 계산원은 25 + 25 + 25 + 5 + 1 + 1 + 1로 7개의 동전을 줄 수 있으며, 이 방법이 최적입니다.
다행히도, 캐나다 화폐 시스템은 탐욕 알고리즘이 항상 최적의 해를 제공하는 성질을 가지고 있습니다. 탐욕 알고리즘은 반복적으로 남은 금액보다 작거나 같은 가장 큰 값을 가진 동전을 선택하는 방식으로 진행합니다. 탐욕 알고리즘이 항상 최적의 해를 제공하는 화폐 시스템을 '정식(canonical)' 화폐 시스템이라고 부릅니다.
여러분의 도전 과제는 다음과 같습니다: 주어진 화폐 시스템 S = {c1, c2, ..., cn}에 대해 S가 정식인지 비정식(non-canonical)인지 판단하는 것입니다. 만약 S가 비정식이라면, 최소한 하나의 반례가 존재하며, 이는 탐욕 알고리즘으로 구한 동전 개수가 최적의 동전 개수보다 많아지는 양의 정수 x입니다.
입력:
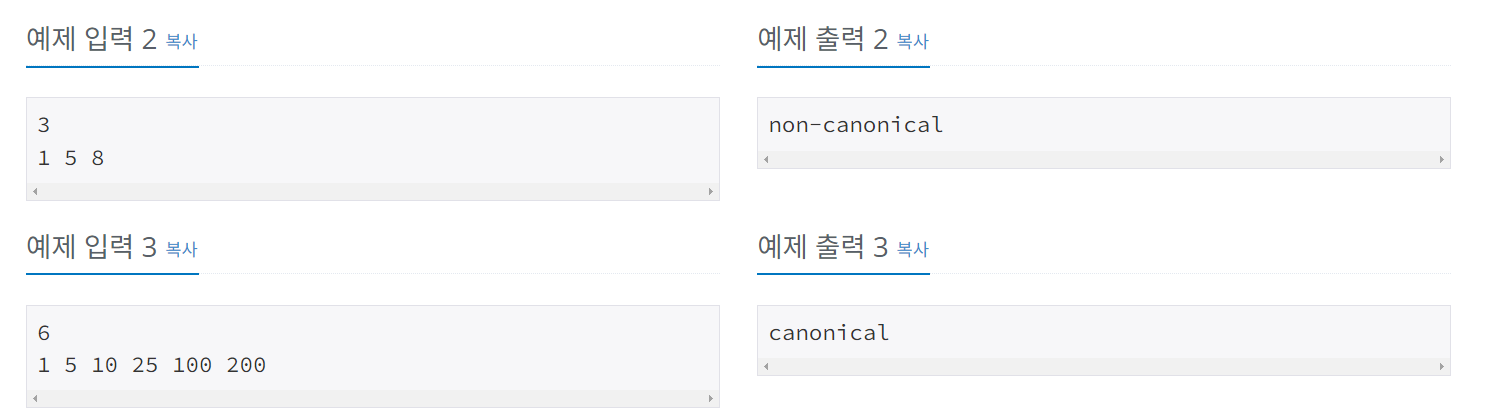
입력은 하나의 경우로 구성됩니다. 첫 번째 줄에는 동전 종류의 수 n (2 ≤ n ≤ 100)이 주어집니다. 다음 줄에는 n개의 동전 값 c1 c2 ... cn이 공백으로 구분되어 주어지며, c1 = 1이고 c1 < c2 < ... < cn ≤ 10^6입니다.
출력:
화폐 시스템이 정식이면 "canonical"을, 비정식이면 "non-canonical"을 출력하세요.
#문제 간단 정리
그리디 + dp 를 구현하라
#문제 해결 방법
우선 딱 보면 알수 있겟지만
그리디를 구현하고
dp를 통한 최적해를 통해서
둘을 비교하면 얻을 수 있다는 것을 알 수 있다.
그리디는 쉽게 구현할 수 있으니 넘어가고
dp는 배낭문제와 같은데
dp[i]는 금액 i을 만들기 위한 최소 동전 수
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
의 점화식을 갖는다
그리고
확인하는 최대 금액이 어째서
int max_x = coins[n-2] + coins[n-1];
인지가 중요한거 같은데
지문에
An example of a non-canonical coin system is {1, 3, 4}, for which 6 is a counterexample, since the greedy algorithm yields 4 + 1 + 1 (3 coins), but an optimal solution is 3 + 3 (2 coins). A useful fact (due to Dexter Kozen and Shmuel Zaks) is that if S is noncanonical, then the smallest counterexample is less than the sum of the two largest denominations.
라고 나와있는데
"예를 들어, {1, 3, 4}라는 비정식(non-canonical) 화폐 시스템에서는 6이 반례(counterexample)가 됩니다. 탐욕 알고리즘을 사용하면 4 + 1 + 1, 즉 3개의 동전이 사용되지만, 최적의 해법은 3 + 3으로 2개의 동전만 필요합니다. Dexter Kozen과 Shmuel Zaks에 따르면, 화폐 시스템이 비정식이라면 가장 작은 반례는 두 개의 가장 큰 동전 값의 합보다 작다는 유용한 사실이 있습니다."
라고 잘 나와잇다.
#전체 코드
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;
vector<int> coins;
int greedy(int value,vector<int> &coins) {
int count = 0;
int remaining = value;
for (int i = coins.size() - 1; i >= 0; i--) {
if (coins[i] <= remaining) {
int num = remaining / coins[i];
count += num;
remaining -= coins[i] * num;
}
if (remaining == 0) {
break;
}
}
return count;
}
int main() {
int n;
cin >> n;
coins.resize(n);
for (int i = 0; i < n; i++) {
cin >> coins[i];
}
sort(coins.begin(), coins.end());
int max_x = coins[n - 2] + coins[n - 1];
vector<int> dp(max_x + 1, max_x + 1);
dp[0] = 0;
for (int i = 1; i <= max_x; i++) {
for (int j = 0; j < n; j++) {
if (coins[j] <= i) {
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
else {
break;
}
}
}
bool isCanonical = true;
for (int x = 1; x <= max_x; ++x) {
int greedy_count = greedy(x, coins);
if (greedy_count > dp[x]) {
isCanonical = false;
break;
}
}
if (isCanonical) {
cout << "canonical" << '\n';
}
else {
cout << "non-canonical" << '\n';
}
return 0;
}'[백준] > C++' 카테고리의 다른 글
| 백준 15812번 침략자 진아 [C++] (0) | 2024.10.02 |
|---|---|
| 백준 24595번 Rise and Fall [C++] (0) | 2024.10.01 |
| 백준 16405번 Birthday Boy [C++] (1) | 2024.09.21 |
| 백준 4040번 Polar Bear [C++] (1) | 2024.09.21 |
| 백준 31747번 점호 [C++] (1) | 2024.09.16 |
